《2025年新课程学习与测评同步学习八年级数学上册人教版》

2. 已知单项式$3x^{2}y^{3}与2xy^{2}的积为6x^{3}y^{n}$,那么$n$的值为(B)。
A.11
B.5
C.1
D.$-1$

答案： B

3. [2023 青海西宁中考]
计算：$3a^{2}b\cdot(-a)^{2}= $3a⁴b。

答案： 3a⁴b

4. [教材第 104 页练习第 4 题变式·跨学科]已知光的速度约为$3×10^{5}km/s$,太阳光照射到地球上需要的时间约为$5×10^{2}s$,则地球与太阳的距离约是1.5×10⁷km。(结果用科学记数法表示)

答案： 1.5×10⁷

5. [教材第 103 页例 1 变式]计算：
(1)$4x^{4}y^{2}\cdot3xy$；
(2)$(-\frac{1}{2}x^{2}y)^{3}\cdot(2xy^{2})^{2}$；
(3)$2a^{2}\cdot a^{4}+(-a^{3})^{2}-3a^{6}$。

答案：
(1)12x⁵y³；
(2)-$\frac{1}{2}$x⁸y⁷；
(3)0

6. 先化简,再求值：$-10(-a^{3}b^{2})^{2}\cdot\frac{1}{5}ab^{3}-(2ab)^{3}\cdot(-a^{2}b^{2})^{2}$,其中$a= -5$,$b= 0.2$。

答案： 解:原式=-10a⁴b⁴·$\frac{1}{5}$ab³-8a³b³·a⁴b⁴=-2a⁵b⁷-8a⁷b⁷=-10a⁷b⁷.当a=-5,b=0.2时,原式=-10×(-5)⁷×(0.2)⁷=-10×[(-5)×0.2]⁷=-10×(-1)⁷=10.

7. [新定义]规定$\begin{array}{c}\triangle\\\end{array}\begin{array}{c}\triangle\\ \begin{array}{c}x\\y\ z\end{array} $表示$3xyz,\begin{array}{c}□\\\end{array}\begin{array}{c}□\\ \begin{array}{c}a\ d\\b\ c\end{array} $表示$-4a^{b}d^{c}。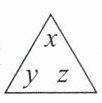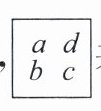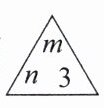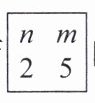$则$\begin{array}{c}\triangle\\\end{array}\begin{array}{c}\triangle\\ \begin{array}{c}m\\n\ 3\end{array} $与$\begin{array}{c}□\\\end{array}\begin{array}{c}□\\ \begin{array}{c}n\ m\\2\ 5\end{array} $的积= -36m⁶n³。

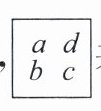
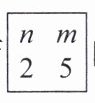
答案： -36m⁶n³

一般地,单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加。

答案： 每一项 相加

1. 计算$a(a + b)$的结果是(C)。
A.$a^{3}+ab$
B.$a^{2}+b$
C.$a^{2}+ab$
D.$2a + ab$

答案： C