第104页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
3. 如图 9,在四边形 $ ABCD $ 中,$ \angle DAB = \angle DCB = 90° $,$ M $,$ N $ 分别是 $ BC $,$ AB $ 边上的动点,$ \angle ADC = 122° $,当 $ \triangle DMN $ 的周长最小时,$ \angle MDN $ 的度数是( )。
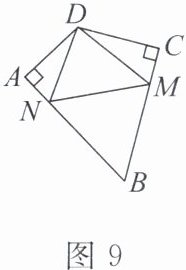
A.$ 122° $
B.$ 64° $
C.$ 62° $
D.$ 58° $

A.$ 122° $
B.$ 64° $
C.$ 62° $
D.$ 58° $

答案:
B 提示:如图85,延长DA到点E,使DA=AE,延长DC到点F,使CF=DC,连接EF,交AB于点N,交BC于点M.则DM=FM,DN=EN,此时△DMN的周长最小.所以∠E=∠ADN,∠F=∠CDM.设∠MDN=α,则∠ADN+∠CDM=122°−α.所以∠DNM+∠DMN=2(122°−α).由三角形的内角和定理,得α+2(122°−α)=180°.解得α=64°.

B 提示:如图85,延长DA到点E,使DA=AE,延长DC到点F,使CF=DC,连接EF,交AB于点N,交BC于点M.则DM=FM,DN=EN,此时△DMN的周长最小.所以∠E=∠ADN,∠F=∠CDM.设∠MDN=α,则∠ADN+∠CDM=122°−α.所以∠DNM+∠DMN=2(122°−α).由三角形的内角和定理,得α+2(122°−α)=180°.解得α=64°.

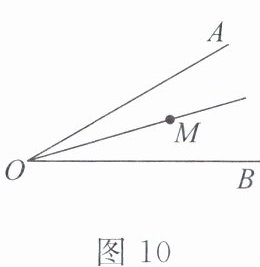
4. 如图 10,$ \angle AOB = 30° $,点 $ M $ 是 $ \angle AOB $ 内任意一个点,$ OM = 5 $,若 $ OA $ 上存在点 $ P $,$ OB $ 上存在点 $ Q $ 使得 $ \triangle MPQ $ 的周长最小,则最小值为 ______。
答案:
5 提示:如图86,作点M关于OA的对称点E,关于OB的对称点F,连接EP,FQ,OE,OF,EF.由轴对称的性质,得PE=PM,MQ=FQ,∠POM=∠POE,∠QOM=∠QOF,OE=OM=OF=5.所以△MPQ的周长=PM+QM+PQ=PE+PQ+FQ≥EF,且当E,P,F,Q四点共线时,△PQM的周长最小,即为EF的长.因为∠AOB=∠POM+∠QOM=30°,所以∠EOF=2∠AOB=60°.
∴ △EOF为等边三角形.所以EF=OE=OF=5,即△MPQ周长的最小值为5.

5 提示:如图86,作点M关于OA的对称点E,关于OB的对称点F,连接EP,FQ,OE,OF,EF.由轴对称的性质,得PE=PM,MQ=FQ,∠POM=∠POE,∠QOM=∠QOF,OE=OM=OF=5.所以△MPQ的周长=PM+QM+PQ=PE+PQ+FQ≥EF,且当E,P,F,Q四点共线时,△PQM的周长最小,即为EF的长.因为∠AOB=∠POM+∠QOM=30°,所以∠EOF=2∠AOB=60°.
∴ △EOF为等边三角形.所以EF=OE=OF=5,即△MPQ周长的最小值为5.

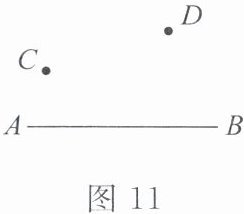
5. (1)如图 11,在直线 $ AB $ 的同一侧有两点 $ C $,$ D $,在 $ AB $ 上找一点 $ P $,使 $ C $,$ D $,$ P $ 三点组成的三角形的周长最小,找出此点。(保留作图痕迹,并说明找点的过程及理由)
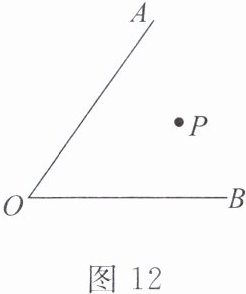
(2)如图 12,在 $ \angle AOB $ 内部有一点 $ P $,在 $ OA $,$ OB $ 上是否分别存在点 $ E $,$ F $,使得 $ E $,$ F $,$ P $ 三点组成的三角形的周长最小,找出 $ E $,$ F $ 两点。(保留作图痕迹,并说明找点的过程及理由)
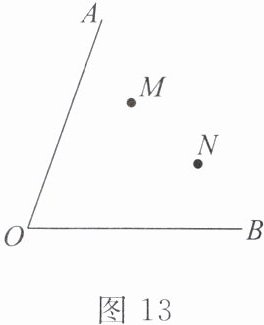
(3)如图 13,在 $ \angle AOB $ 内部有 $ M $,$ N $ 两点,在 $ OA $,$ OB $ 上是否分别存在点 $ E $,$ F $,使得 $ E $,$ F $,$ M $,$ N $ 四点组成的四边形的周长最小,找出 $ E $,$ F $ 两点。(保留作图痕迹,并说明找点的过程及理由)

(2)如图 12,在 $ \angle AOB $ 内部有一点 $ P $,在 $ OA $,$ OB $ 上是否分别存在点 $ E $,$ F $,使得 $ E $,$ F $,$ P $ 三点组成的三角形的周长最小,找出 $ E $,$ F $ 两点。(保留作图痕迹,并说明找点的过程及理由)

(3)如图 13,在 $ \angle AOB $ 内部有 $ M $,$ N $ 两点,在 $ OA $,$ OB $ 上是否分别存在点 $ E $,$ F $,使得 $ E $,$ F $,$ M $,$ N $ 四点组成的四边形的周长最小,找出 $ E $,$ F $ 两点。(保留作图痕迹,并说明找点的过程及理由)

答案:
5.解:
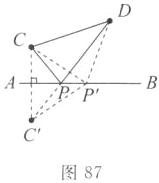
(1)如图87,作点C关于直线AB的对称点C',连接C'D交AB于点P.则点P就是所求作的点.理由:在AB上取不同于点P的点P',连接CP',DP',C'P'.
∵ C和C'关于直线AB对称,
∴ CP=C'P,CP'=C'P'.而C'P+DP<C'P'+DP',
∴ CP+DP<CP'+DP',
∴ CD+CP+DP<CD+CP'+DP',即△CDP的周长小于△CDP'的周长.
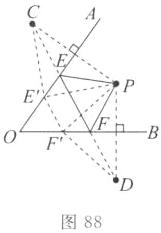
(2)如图88,作点P关于OA的对称点C,关于OB的对称点D,连接CD,交OA于点E,OB于点F,则点E,F就是所求作的点.理由:分别在OA,OB上取不同于点E,F的点E',F',连接PE,PF,CE',PE',PF',DF',E'F'.
∵ 点C和点P关于直线OA对称,点D和点P关于直线OB对称,
∴ PE=CE,CE'=PE',PF=DF,PF'=DF'.
∴ PE+EF+PF=CE+EF+DF,PE'+E'F'+PF'=CE'+E'F'+DF'.
∵ CE+EF+DF<CE'+E'F'+DF',
∴ PE+EF+PF<PE'+E'F'+PF',即△PEF的周长小于△PE'F'的周长.
(3)如图89,作点M关于OA的对称点C,作点N关于OB的对称点D,连接CD,交OA于点E,OB于点F,则点E,F就是所求作的点.理由:分别在OA,OB上取不同于点E,F的点E',F',连接ME,NF,CE',E'F',DF',ME',NF'.
∵ 点C和点M关于直线OA对称,点N和点D关于直线OB对称,
∴ ME=CE,CE'=ME',NF=DF,NF'=DF'.同
(2)可得,MN+ME+EF+NF<MN+ME'+E'F'+F'N,即四边形MEFN的周长小于四边形ME'F'N的周长.

5.解:
(1)如图87,作点C关于直线AB的对称点C',连接C'D交AB于点P.则点P就是所求作的点.理由:在AB上取不同于点P的点P',连接CP',DP',C'P'.
∵ C和C'关于直线AB对称,
∴ CP=C'P,CP'=C'P'.而C'P+DP<C'P'+DP',
∴ CP+DP<CP'+DP',
∴ CD+CP+DP<CD+CP'+DP',即△CDP的周长小于△CDP'的周长.

(2)如图88,作点P关于OA的对称点C,关于OB的对称点D,连接CD,交OA于点E,OB于点F,则点E,F就是所求作的点.理由:分别在OA,OB上取不同于点E,F的点E',F',连接PE,PF,CE',PE',PF',DF',E'F'.
∵ 点C和点P关于直线OA对称,点D和点P关于直线OB对称,
∴ PE=CE,CE'=PE',PF=DF,PF'=DF'.
∴ PE+EF+PF=CE+EF+DF,PE'+E'F'+PF'=CE'+E'F'+DF'.
∵ CE+EF+DF<CE'+E'F'+DF',
∴ PE+EF+PF<PE'+E'F'+PF',即△PEF的周长小于△PE'F'的周长.

(3)如图89,作点M关于OA的对称点C,作点N关于OB的对称点D,连接CD,交OA于点E,OB于点F,则点E,F就是所求作的点.理由:分别在OA,OB上取不同于点E,F的点E',F',连接ME,NF,CE',E'F',DF',ME',NF'.
∵ 点C和点M关于直线OA对称,点N和点D关于直线OB对称,
∴ ME=CE,CE'=ME',NF=DF,NF'=DF'.同
(2)可得,MN+ME+EF+NF<MN+ME'+E'F'+F'N,即四边形MEFN的周长小于四边形ME'F'N的周长.

查看更多完整答案,请扫码查看


