《2025年能力培养与测试八年级物理上册教科版》

8. 一种身高测量仪如图3-4-3所示，其顶部的感应器竖直向下发射超声波信号，经下方物体反射后返回，被感应器接收。某同学站上测高台，感应器记录信号从发射到接收所经历的时间为5×10⁻³s。已知感应器到测高台的距离为2.5m，空气中的声速取340m/s。则该同学的身高为1.65m。(对应目标：813405)

答案： 1.65

答案： 当列车驶向山崖时，会先穿过桥梁，再鸣笛，声波传到山崖再反射回来，形成回声被列车接收。
假设声速为$v_s$，列车速度为$v$，列车从桥头到山崖的距离为$S$。
声音从山崖反射到桥尾的距离为桥长加上列车移动的距离，即：
$2S + L = v_s \cdot t$，
其中，$L$为桥长，$t$为声音传播的时间。
列车在时间$t$内行驶的距离为：
$S_{列车} = v \cdot t$，
由于列车在时间$t$内行驶的距离加上桥长等于声音传播的距离减去桥尾到山崖的距离，即：
$v \cdot t + L = v_s \cdot t - S$（此式不便于计算），
通常我们设当列车不移动时，即$v = 0$，则：
$t = \frac{2S}{v_s}$，
但题目中列车是移动的，因此需要考虑多普勒效应或相对运动。
简化考虑，假设列车在鸣笛瞬间与山崖的距离为$S$，则回声到达时列车已经移动了$v \cdot t$，此时：
$t = \frac{2S}{v_s + v}$（对于接近运动），
或$t = \frac{2S}{v_s - v}$（对于远离运动，但本题是接近）。
由于题目要求的是基于八年级物理知识，通常采用简化模型，即假设列车速度远小于声速，因此可以近似为：
$t \approx \frac{2S}{v_s}$，
但严格解应为：
$t = \frac{2S}{v_s + v}$。
最终，列车从桥头驶向山崖时，听到回声的时间$t$为：
$t = \frac{2S}{v_s + v}$。

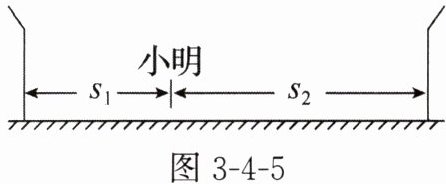
10. 如图3-4-5所示，有一山谷宽1700m，两旁都是垂直的山崖，小明在山谷里某处大喊一声，他听到了一连串的回声，前两次回声间隔4s。求小明到两旁山崖的距离。（取空气中的声速为340m/s）（对应目标：813401，813405）

答案： 解：由题可知小明听到第一次回声的时间t₁= 2s₁/v，小明听到第二次回声的时间t₂= 2s₂/v，其中s₁+s₂=1700 m根据题意可知t₂-t₁=4 s，解得s₁=510 m，s₂=1190 m。

11. 在某段区间测速路段，交管部门在公路上设置了固定测速仪。如图3-4-6所示，汽车向放置在路中的测速仪匀速驶来，测速仪从第一次发出超声波信号到接收到信号用时0.8s，从第二次发出信号到接收到信号用时0.6s。已知两次发出信号的间隔时间是2.1s，声音在空气中的传播速度为340m/s，求：（对应目标：813401，813405）
（1）超声波在空气中传播0.8s通过的路程。
（2）汽车反射第一次信号时到测速仪的距离。
（3）汽车从反射第一次信号到反射第二次信号间行驶的路程。
（4）汽车行驶的速度。

答案： （1）超声波在空气中传播0.8 s通过的路程s₁=v声t₁=340 m/s×0.8 s=272 m；
（2）当汽车反射第一次信号时，汽车到测速仪的距离s₁'=1/2 s₁=1/2×272 m=136 m；
（3）测速仪第二次发出信号到接收到信号用时0.6 s，所以测速仪发出的第二次信号到达汽车的时间t₂'=1/2 t₂=1/2×0.6 s=0.3 s，当汽车反射第二次信号时，汽车到测速仪的距离s₂=v声t₂'=340 m/s×0.3 s=102 m，汽车从反射第一次信号到反射第二次信号间行驶的路程s'=s₁'-s₂=136 m-102 m=34 m；
（4）这34 m共耗用时间t'=2.1 s-0.4 s+0.3 s=2 s，所以汽车的车速v= s'/t'=34 m/2 s=17 m/s。