18. 一门反坦克炮瞄准一辆坦克,开炮后经过 0.6 s 看到炮弹在坦克上爆炸,再经过 2.1 s 听到爆炸的声音(声音在空气中传播的速度为 340 m/s)。求:
(1)大炮与坦克间的距离。
(2)炮弹飞行的速度。
(1)大炮与坦克间的距离。
(2)炮弹飞行的速度。
答案:
(1)714 m (2)1190 m/s
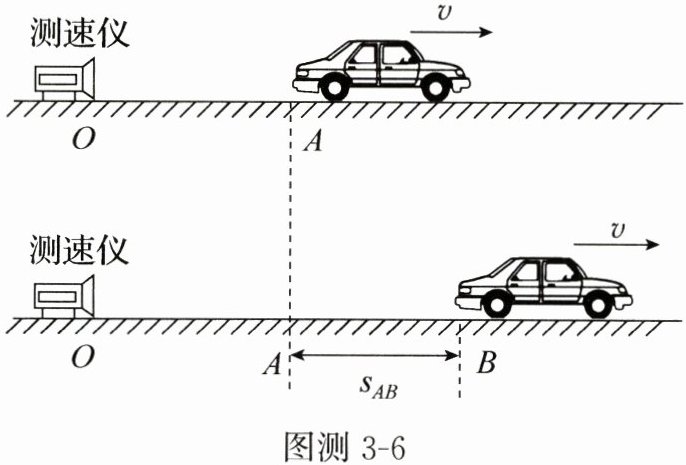
19. 超声波测速仪发出超声波脉冲信号,遇到汽车发生反射,通过分析发出和接收到信号的时间差,可计算出汽车的速度。如图测 3 - 6 所示,在限速为 80 km/h 的直线路段,交警架设了超声波测速仪测汽车速度。当行驶的汽车距离测速仪$ s_{OA} = 62 m $时,测速仪向汽车发出超声波,超声波“追上”汽车时,汽车刚好运动到 B 点。测速仪从发出到接收反射回来的超声波所用的时间是 0.4 s。已知超声波传播的速度为 340 m/s。
(1)求经过 0.4 s 超声波传播的路程。
(2)求汽车运动的路程$ s_{AB}。$
(3)通过计算说明汽车在此路段是否超速。
(1)求经过 0.4 s 超声波传播的路程。
(2)求汽车运动的路程$ s_{AB}。$
(3)通过计算说明汽车在此路段是否超速。

答案:
解:(1)经过0.4 s超声波通过的路程$s_{1}=v_{1}t=340\ m/s×0.4\ s=136\ m$;(2)这段时间里,汽车通过的路程$s_{AB}=s_{OB}-s_{OA}=\frac{1}{2}s_{1}-s_{OA}=\frac{1}{2}×136\ m-62\ m=6\ m$;(3)汽车通过AB段所需的时间$t_{车}=\frac{1}{2}t=\frac{1}{2}×0.4\ s=0.2\ s$,汽车在此段路的速度$v_{2}=\frac{s_{AB}}{t_{车}}=\frac{6\ m}{0.2\ s}=30\ m/s=108\ km/h>80\ km/h$,所以汽车已经超速了。
20. 一辆汽车面向一座高山以 36 km/h 的速度匀速行驶时,鸣笛 4 s 后听到回声,求:
(1)这段时间内汽车前进的距离。
(2)这段时间内声音传播的距离。
(3)司机听到回声时到高山的距离。(声音在空气中传播的速度是 340 m/s)
(1)这段时间内汽车前进的距离。
(2)这段时间内声音传播的距离。
(3)司机听到回声时到高山的距离。(声音在空气中传播的速度是 340 m/s)
答案:
解:(1)汽车的速度$v_{车}=36\ km/h=10\ m/s$,由$v=\frac{s}{t}$可知,这段时间内汽车通过的路程$s_{车}=v_{车}t=10\ m/s×4\ s=40\ m$;(2)这段时间内声音传播的路程$s_{声}=v_{声}t=340\ m/s×4\ s=1360\ m$;(3)司机听到回声时,汽车到高山的距离$s=\frac{1}{2}(s_{声}-s_{车})=\frac{1}{2}×(1360\ m-40\ m)=660\ m$。
查看更多完整答案,请扫码查看


