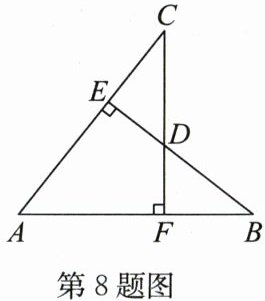
8. (2024·南京秦淮区期末)如图,$AB = AC$,$BE\perp AC$,$CF\perp AB$,垂足分别为$E$,$F$,$CF与BE交于点D$,下列结论:①$\triangle ABE\cong\triangle ACF$;②$\triangle BDF\cong\triangle CDE$;③点$D在\angle BAC$的平分线上;④$AB = DF + DB$.其中所有正确结论的序号是(
A.①②
B.②③
C.①②③
D.①②③④
C
)
A.①②
B.②③
C.①②③
D.①②③④
答案:
C
9. (2024·宿城期中)在$\triangle ABC$中,$\angle A = 45^{\circ}$,$\angle B = 60^{\circ}$.若$\triangle ABC\cong\triangle DEF$,则$\angle F$的度数为
75°
.
答案:
75°
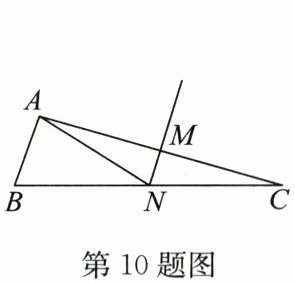
10. (2024·宿城期中)如图,在$\triangle ABC$中,边$AC的垂直平分线交AC于点M$,交$BC于点N$.若$AB = 3$,$BC = 13$,则$\triangle ABN$的周长是
16
.
答案:
16
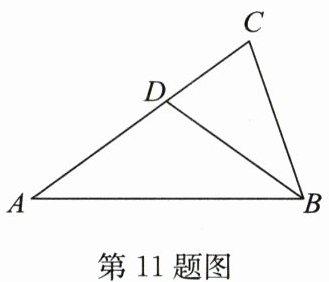
11. (2024·重庆B卷)如图,在$\triangle ABC$中,$AB = AC$,$\angle A = 36^{\circ}$,$BD平分\angle ABC交AC于点D$.若$BC = 2$,则$AD$的长为______.

2
答案:
2
12. 等腰三角形的一个内角为$50^{\circ}$,那么这个等腰三角形的一个底角的度数为
50°或65°
.
答案:
50°或65°
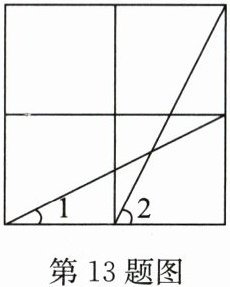
13. 如图,已知方格纸中是4个相同的小正方形,则$\angle 1+\angle 2$的度数为
90°
.
答案:
90°
14. 如图,在$\triangle ABC$中,$\angle CAD= \angle EAD$,$\angle ADC= \angle ADE$,$CB = 5\mathrm{cm}$,$BD = 3\mathrm{cm}$,则$ED$的长为
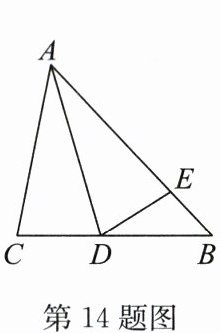
2
$\mathrm{cm}$.
答案:
2
15. (2024·南京浦口区期末)如图,等边$\triangle ABC$中,$AD是BC$边上的中线,且$AD = 17$,$E$,$P分别是AC$,$AD$上的动点,则$CP + EP$的最小值等于
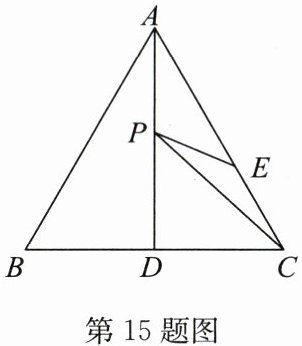
17
.
答案:
17
16. 如图,在等腰直角三角形$ABC$中,$\angle BAC = 90^{\circ}$,$D是AC$的中点,$CE\perp BD于点E$,交$BA的延长线于点F$,若$BF = 12$,则$\triangle FBC$的面积为
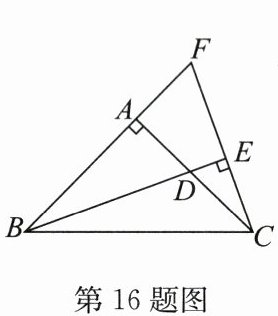
48
.
答案:
48
17. (6分)如图,点$E$,$F在线段CD$上,且$CE = DF$,$AE = BF$,$AE// BF$.求证:$\triangle AEC\cong\triangle BFD$.
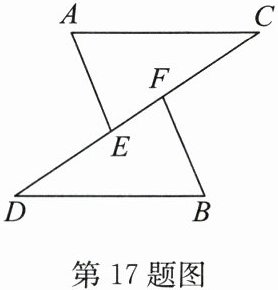

答案:
证明:
∵AE//BF,
∴∠AEC=∠BFD.又
∵CE=DF,AE=BF,
∴△AEC≌△BFD(SAS).
∵AE//BF,
∴∠AEC=∠BFD.又
∵CE=DF,AE=BF,
∴△AEC≌△BFD(SAS).
查看更多完整答案,请扫码查看


