4. 在$\triangle ABC$中,$\angle A-\angle B = 90^{\circ}$,$\angle B = 2\angle C$,求$\triangle ABC$的各内角的度数.
答案:
解 设∠C=x°,则∠B=2x°,∠A=90°+∠B=(90+2x)°.∠A+∠B+∠C=180°,即90+2x+2x+x=180,解得x=18.所以∠A=(90+2×18)°=126°,∠B=2×18°=36°,∠C=18°.所以△ABC的各内角的度数分别为∠A=126°,∠B=36°,∠C=18°.
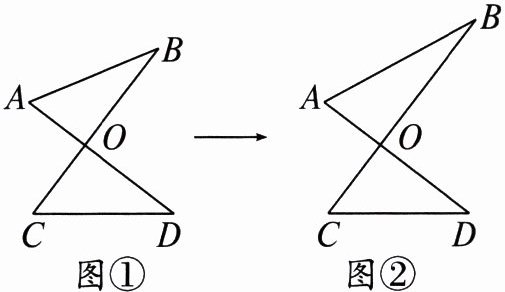
5. 明明在电脑上用画图软件画出的图形如图①,$AD与BC交于点O$,若他拖动图形,使得$\angle B的度数减小了6^{\circ}$,$\angle A的度数增加了6^{\circ}$,得到的图形如图②,设图①中$\angle C+\angle D的度数为x^{\circ}$,图②中$\angle C+\angle D的度数为y^{\circ}$,则$x与y$的数量关系为( )
A.$x = y$
B.$x = y - 6$
C.$x = y + 6$
D.$x = y - 12$

A.$x = y$
B.$x = y - 6$
C.$x = y + 6$
D.$x = y - 12$
答案:
A
6. 如图,$\angle 1+\angle 2+\angle 3+\angle 4= $______.
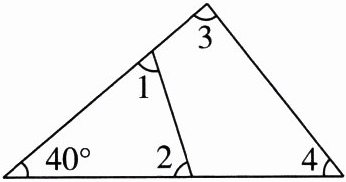

答案:
280°
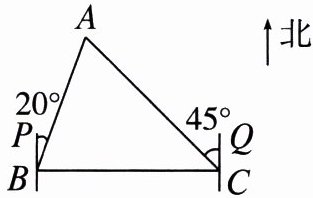
7. 某地有$A$,$B$,$C$三个村庄,如图,$B村庄在C$村庄的正西方向,$A村庄在B村庄的北偏东20^{\circ}$方向,同时$A村庄又在C村庄的北偏西45^{\circ}$方向,那么$\angle BAC$的度数为多少?

答案:
解 由题意可得∠PBC=∠QCB=90°,∠ABC=∠PBC-∠PBA=90°-20°=70°,∠ACB=∠QCB-∠ACQ=90°-45°=45°,
∴∠BAC=180°-∠ABC-∠ACB=180°-70°-45°=65°,
∴∠BAC的度数是65°.
∴∠BAC=180°-∠ABC-∠ACB=180°-70°-45°=65°,
∴∠BAC的度数是65°.
查看更多完整答案,请扫码查看


