《2025年同步测控优化设计八年级数学上册人教版福建专版》

7. 如图,在△ABC中,AD是BC边上的中线,△ABD的周长比△ADC的周长多2,且AB与AC的和为10。
(1)求AB,AC的长；

(2)求BC边的取值范围。

答案：
(1)$\because AD$是$BC$边上的中线,
$\therefore BD=CD$,$\therefore \triangle ABD$的周长$-\triangle ADC$的周长$=$
$(AB+AD+BD)-(AC+AD+CD)=AB-AC=2$,即
$AB-AC=2$①,又$AB+AC=10$②,
由①+②,得$2AB=12$,解得$AB=6$,
由②-①,得$2AC=8$,解得$AC=4$,
$\therefore AB=6$,$AC=4$.
(2)$\because AB=6$,$AC=4$,$\therefore 2＜BC＜10$.

1. 三角形的内角和
三角形的内角和等于______.

答案： 180°

2. 三角形内角和的证明方法及思路
(1)度量法：用量角器测量.
(2)剪拼法：将三个内角拼在一个顶点处,合起来形成一个平角.

(3)利用平行线的性质与平角的定义证明.
原理：运用平行线的性质,将三角形的三个内角转化为一个平角或者一对同旁内角.

答案： （回答合理即可，本题无选项）

1. 根据图中的数据,可得$x + y$的值为( )


A.180
B.110
C.100
D.70

答案： B

2. 如图,在$\triangle ABC$中,点$D$,$E分别在AB$,$AC$上,$DE// BC$,若$\angle B = 70^{\circ}$,$\angle AED = 50^{\circ}$,则$\angle A$的度数为______.

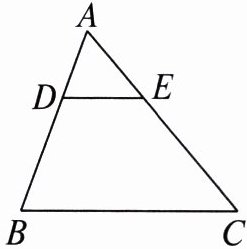
答案： 60°

3. 如图,在$\triangle ABC$中,$CE平分\angle ACB$,$\angle 1= \angle 2$,若$\angle ACE = 23^{\circ}$,求$\angle EDC$的度数.

答案： 解
∵CE平分∠ACB，∠ACE=23°，
∴∠2=∠1=∠ACE=23°，
∴∠EDC=180°-∠1-∠2=180°-23°-23°=134°.