《2025年同步测控优化设计八年级数学上册人教版福建专版》

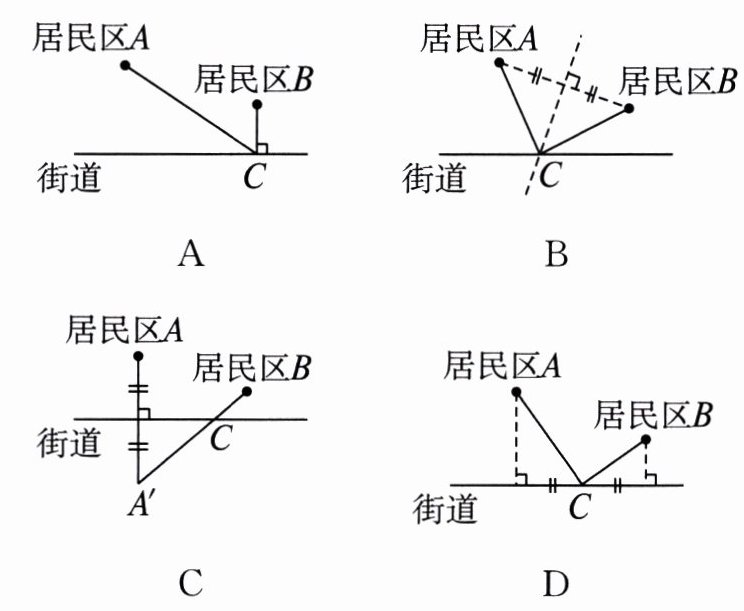
1. 小王准备在街道旁建一个送奶站,向居民区 $ A $,$ B $ 提供牛奶,要使 $ A $,$ B $ 两小区到送奶站的距离之和最小,则送奶站 $ C $ 的位置应该在( )

答案： C

2. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ AD $,$ CE $ 是 $ \triangle ABC $ 的两条中线,$ P $ 是 $ AD $ 上的一个动点,则下列线段的长等于 $ BP + EP $ 最小值的是( )


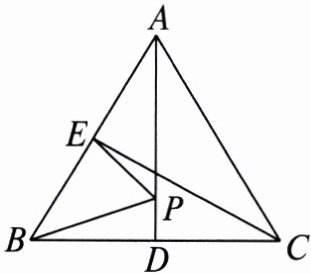
A.$ BC $
B.$ CE $
C.$ AD $
D.$ AC $

答案： B

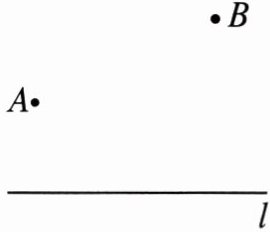
3. 如图,要在燃气管道 $ l $ 上修建一个泵站,分别向 $ A $,$ B $ 两处供气,泵站修在管道的什么位置可使所用的输气管线最短？请说明理由。

答案：
解 如图，作点A关于直线l的对称点A'，连接A'B交直线l于点P，连接AP，则泵站修在管道的P点处，可使所用的输气管线AP+BP最短.

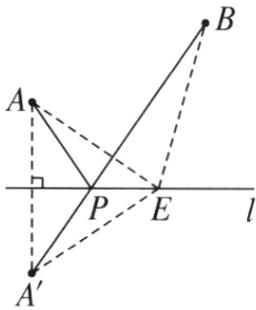
理由:
在直线l上任取一点E，连接AE，BE，A'E.
∵A，A'关于直线l对称，
∴AP=A'P.
同理AE=A'E.
∵AP+BP=A'P+BP=A'B，
AE+BE=A'E+BE＞A'B，
∴AP+BP＜AE+BE.
∵E是任意取的一点，
∴AP+BP最短.