《2025年同步测控优化设计八年级数学上册人教版福建专版》

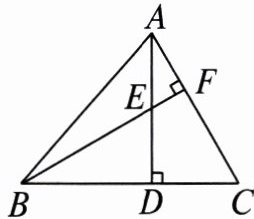
5. 如图,在$\triangle ABC$中,$\angle C = 60^{\circ}$,$AD是BC$边上的高,$E为AD$的中点,连接$BE并延长交AC于点F$.若$\angle AFB = 90^{\circ}$,$EF = 2$,求$BF$的长.

答案： 解
∵在△ABC 中,∠C=60°,AD 是 BC 边上的高,
∴∠DAC=90°-∠C=90°-60°=30°.
∵∠AFB=90°,EF=2,
∴AE=2EF=4.
∵点 E 为 AD 的中点,
∴DE=AE=4.
∵∠C=60°,∠BFC=90°,
∴∠EBD=30°,
∴BE=2DE=8,
∴BF=BE+EF=8+2=10.

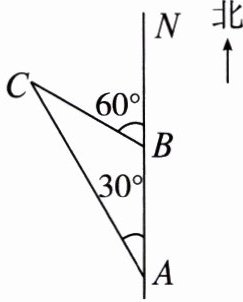
6. 上午8时,一条船从海岛$A$出发,以15海里/时的速度向正北航行,上午10时到达海岛$B$处,从$A$,$B望灯塔C$,测得$\angle NAC = 30^{\circ}$,$\angle NBC = 60^{\circ}$.
(1)求从海岛$B到灯塔C$的距离；
(2)这条船继续向正北航行,在什么时间小船与灯塔$C$的距离最短？

答案：
(1)
∵∠NBC=60°,∠NAC=30°,
∴∠ACB=60°-30°=30°,
∴AB=BC.
∵AB=15×2=30(海里),
∴从海岛 B 到灯塔 C 的距离为 30 海里.
(2)如图,过点 C 作 CP⊥AN 于点 P,故小船在点 P 处与灯塔 C 的距离最短.
∵∠NBC=60°,∠BPC=90°,
∴∠PCB=90°-60°=30°,
∴PB=$\frac{1}{2}$BC=15(海里),
15÷15=1(时),
∴这条船继续向正北航行,在上午的 11 时小船与灯塔 C 的距离最短.

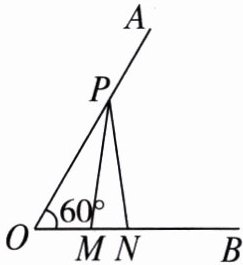
7. 如图,已知$\angle O = 60^{\circ}$,点$P在边OA$上,$OP = 8$,点$M$,$N在边OB$上,$PM = PN$,若$MN = 2$,求$ON$的长.

答案： 解 过点 P 作 PD⊥OB 于点 D,
∵∠ODP=90°,∠O=60°,
∴∠OPD=30°,
∴OD=$\frac{1}{2}$OP=$\frac{1}{2}$×8=4.
∵PM=PN,PD⊥MN,MN=2,
∴MD=ND=$\frac{1}{2}$MN=1,
∴ON=OD+DN=4+1=5.