含$30^{\circ}$角的直角三角形的性质
在直角三角形中,如果一个锐角等于
$30^{\circ}$,那么它所对的直角边等于斜边的______.
在直角三角形中,如果一个锐角等于
$30^{\circ}$,那么它所对的直角边等于斜边的______.
答案:
一半
1. 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$CD是斜边AB$上的高,$\angle ACD = 30^{\circ}$,那么下列结论正确的是( )
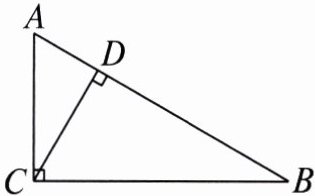
A.$AD = \frac{1}{2}CD$
B.$AC = \frac{1}{2}AB$
C.$BD = \frac{1}{2}BC$
D.$CD = \frac{1}{2}AB$

A.$AD = \frac{1}{2}CD$
B.$AC = \frac{1}{2}AB$
C.$BD = \frac{1}{2}BC$
D.$CD = \frac{1}{2}AB$
答案:
B
2. 如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 3$,$\angle B = 30^{\circ}$,$P是BC$边上的动点,则$AP$的长可能是( )
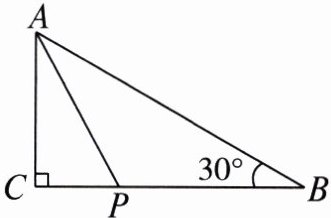
A.$5$
B.$6.2$
C.$7.8$
D.$8$

A.$5$
B.$6.2$
C.$7.8$
D.$8$
答案:
A
3. 如图,已知$AD是\triangle ABC$的中线,$\angle 1 = 2\angle 2$,$CE \perp AD于点E$,$BF \perp AD$,交$AD的延长线于点F$.若$EF = 6$,则$BC = $______.
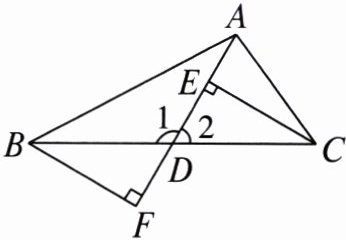

答案:
12
4. 如图,在$Rt\triangle ABC$中,$\angle B = 90^{\circ}$,$\angle ACB = 60^{\circ}$,$DE是斜边AC$的垂直平分线,分别交$AB$,$AC于D$,$E$两点.若$BD = 2$,求$AD$的长.


答案:
解
∵∠ACB=60°,∠B=90°,
∴∠A=30°.
∵DE 是斜边 AC 的垂直平分线,
∴AD=CD,
∴∠ACD=∠A=30°,
∴∠BCD=30°.
∵BD=2,
∴AD=CD=4.
∵∠ACB=60°,∠B=90°,
∴∠A=30°.
∵DE 是斜边 AC 的垂直平分线,
∴AD=CD,
∴∠ACD=∠A=30°,
∴∠BCD=30°.
∵BD=2,
∴AD=CD=4.
查看更多完整答案,请扫码查看


