《2025年同步测控优化设计八年级数学上册人教版福建专版》

7. 如图,在△ABC中,∠ABC和∠ACB的平分线交于点F,过点F作DE//BC,交AB于点E,交AC于点D.

(1)试确定BE,DE,CD之间的数量关系,并说明理由;
(2)若AB+AC= a,求△AED的周长.

答案：
(1)DE=BE+CD.
理由:
∵BF平分∠ABC,CF平分∠ACB，
∴∠EBF=∠CBF,∠DCF=∠BCF.
∵DE//BC,
∴∠EFB=∠CBF,∠DFC=∠BCF，
∴∠EFB=∠EBF,∠DFC=∠DCF，
∴BE=EF,CD=DF.
∵DE=EF+DF,
∴DE=BE+CD.
(2)
∵AB+AC=a,
∴AE+BE+AD+CD=a.
∵由
(1)得ED=BE+CD，
∴AE+AD+ED=a,
∴△AED的周长为a.

1. 等边三角形的性质
等边三角形的三个角都____,并且每一个角都等于____。

答案： 相等　60°

2. 等边三角形的判定
(1)三边都____的三角形是等边三角形。
(2)三个角都____的三角形是等边三角形。
(3)有一个角是____的等腰三角形是等边三角形。

答案：
(1)相等　
(2)相等　
(3)60°

1. 如图,一张等边三角形形状的纸片,剪去一个角后得到一个四边形,则图中∠α + ∠β 的度数是( )


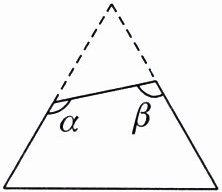
A.$180^{\circ}$
B.$220^{\circ}$
C.$240^{\circ}$
D.$300^{\circ}$

答案： C

2. 已知在△ABC 中,AB = AC,下列结论：
①若 AB = BC,则△ABC 是等边三角形；
②若∠A = $60^{\circ}$,则△ABC 是等边三角形；
③若∠B = $60^{\circ}$,则△ABC 是等边三角形。
其中正确的有( )

A.0 个
B.1 个
C.2 个
D.3 个

答案： D

3. 如图,在等边三角形 ABC 中,AD 是 BC 边上的中线,DE⊥AB 于点 E,DF⊥AC 于点 F,若 DE = 2,则 DF = ____。

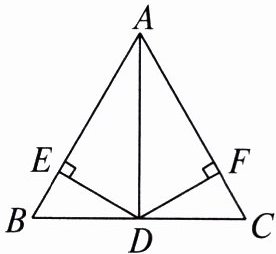
答案： 2