《2025年同步测控优化设计八年级数学上册人教版福建专版》

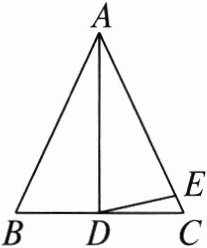
4. 如图,在△ABC中,AB= AC,AD为BC边上的中线,∠BAD= 25°,AE= AD,求∠EDC的度数.

答案： 解：
∵在△ABC中,AB=AC,AD为BC边上的中线,
∴AD平分∠BAC,且AD⊥BC，
∴∠DAC=∠BAD=25°,∠ADC=90°,
∵AE=AD，
∴∠ADE=$\frac{180°-\angle DAC}{2}=\frac{180°-25°}{2}=77.5°$，
∴∠EDC=∠ADC-∠ADE=90°-77.5°=12.5°.

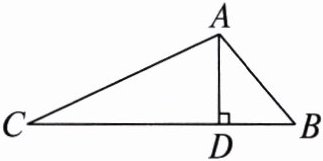
5. 如图,在△ABC中,∠C= 25°,AD⊥BC,垂足为D,且AB+BD= CD,求∠BAC的度数.

答案：
解：延长DB至点E，使BE=AB,连接AE，
∵AB+BD=CD，
∴BE+BD=CD，
即DE=CD，
∴∠C=∠E=25°.
∵BE=AB，
∴∠ABC=2∠E=50°，
∴∠BAC=180°-∠C-∠ABC=180°-25°-50°=105°.

等腰三角形的判定
有两个角____的三角形是等腰三
角形(简写成“等角对____”).

答案： 相等 等边

1. 在下列条件中,可以判定△ABC是等腰三角形的是( )

A.∠B= 40°,∠C= 80°
B.∠A:∠B:∠C= 1:2:3
C.2∠A= ∠B+∠C
D.∠A:∠B:∠C= 2:2:1

答案： D

2. 如图,一艘海轮位于灯塔P的南偏东70°方向的M处,它以40海里每小时的速度向正北方向航行,两个小时后到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为____海里.

答案： 80