《2025年同步测控优化设计八年级数学上册人教版福建专版》

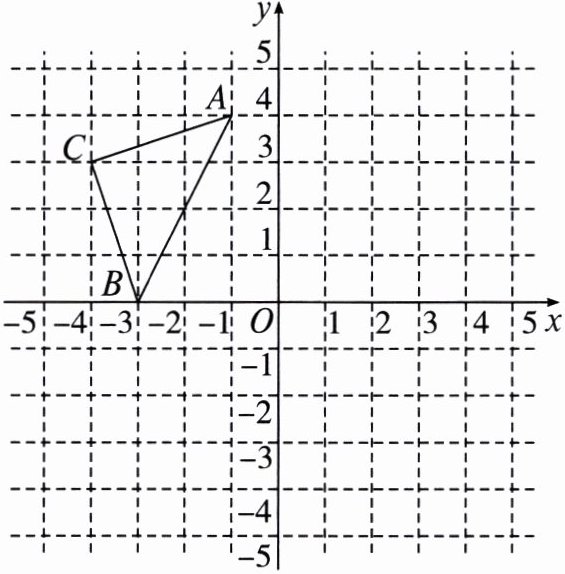
5. 如图,在平面直角坐标系中,$A(-1,4)$,$B(-3,0)$,$C(-4,3)$,网格上最小的正方形的边长为$1$.
(1)画出$\triangle ABC关于y轴对称的图形\triangle A_{1}B_{1}C_{1}$,并写出$A_{1}$,$B_{1}$,$C_{1}$的坐标；
(2)若在$x轴上存在点M$,使得$\triangle MAB的面积为6$,请求出点$M$的坐标.

答案：
5.解
(1)如图.

由图可知,$A_{1}(1,4),B_{1}(3,0),C_{1}(4,3).$
(2)设点M的坐标为$(x,0),$
则$\frac {1}{2}×|x-(-3)|×4=6,$
解得$x=-6$或$x=0,$
则点M的坐标为$(0,0)$或$(-6,0).$

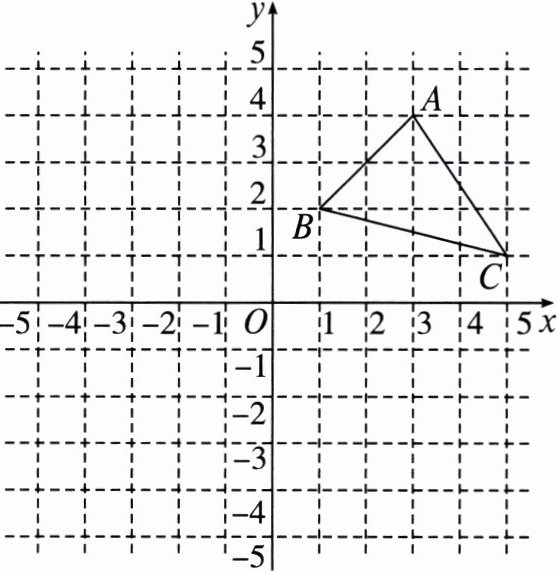
6. 如图,在平面直角坐标系中,$\triangle ABC$的顶点在网格线交点上,最小正方形的边长为$1$.
(1)分别画出$\triangle ABC关于y轴和x轴对称的图形\triangle A_{1}B_{1}C_{1}和\triangle A_{2}B_{2}C_{2}$；
(2)直接写出点$C_{1}$的坐标；
(3)若$P(a,a - 1)是\triangle ABC$内部一点,点$P关于y轴对称的点为P'$,且$PP' = 6$,求点$P'$的坐标.

答案：
6.解
(1)如图,$△A_{1}B_{1}C_{1}$和$△A_{2}B_{2}C_{2}$即为所求.

(2)点$C_{1}$的坐标为$(-5,1).$
(3)
∵点$P(a,a-1)$关于y轴的对称点为$P',$
∴$P'(-a,a-1).$
∵$PP'=6,$
∴$a-(-a)=6,$
∴$a=3$,
∴点$P'$的坐标为$(-3,2).$