《2025年同步测控优化设计八年级数学上册人教版福建专版》

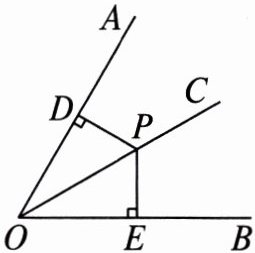
3. 如图,在平面内画 $ \angle AOB $,在 $ OA $,$ OB $ 上分别截取 $ OD $,$ OE $,使 $ OD = OE $,过点 $ D $ 作 $ OD $ 的垂线,过点 $ E $ 作 $ OE $ 的垂线. 若两条垂线相交于点 $ P $,则点 $ P $ 在 $ \angle DOE $ 的平分线上吗？为什么？

答案： 解 点P在$∠DOE$的平分线上，理由：$\because OD⊥PD,OE⊥PE,OD=OE,$$\therefore PO$平分$∠DPE$,即$∠DPO=∠EPO,$$\because DP⊥OD,PE⊥OE,$$\therefore 90^{\circ }-∠DPO=90^{\circ }-∠EPO,$即$∠DOP=∠EOP,\therefore OP$为$∠DOE$的平分线,即点P在$∠DOE$的平分线上.

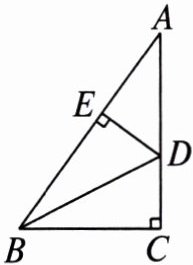
4. 如图,在 $ Rt \triangle ABC $ 中,$ \angle C = 90^{\circ} $,$ D $ 是 $ AC $ 上一点,$ DE \perp AB $ 于点 $ E $,且 $ DE = DC $.
(1)求证：$ BD $ 平分 $ \angle ABC $；
(2)若 $ \angle A = 36^{\circ} $,求 $ \angle DBC $ 的度数.

答案：
(1)证明$\because DC⊥BC,DE⊥AB,DE=DC,$
∴点D在$∠ABC$的平分线上,$\therefore BD$平分$∠ABC.$
(2)解$\because ∠C=90^{\circ },∠A=36^{\circ },\therefore ∠ABC=54^{\circ }.$
∵BD平分$∠ABC,\therefore ∠DBC=\frac {1}{2}∠ABC=27^{\circ }.$

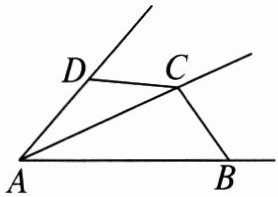
5. 如图,$ \angle ADC + \angle ABC = 180^{\circ} $,$ DC = BC $. 求证：点 $ C $ 在 $ \angle DAB $ 的平分线上.

答案：
证明 如图,作CE垂直AB,CF垂直AD的延长线,垂足分别为E,F,$\therefore ∠BEC=∠DFC=90^{\circ }.$
∵$∠ADC+∠ABC=180^{\circ },∠ADC+∠CDF=180^{\circ },\therefore ∠ABC=∠CDF.$在$\triangle CBE$和$\triangle CDF$中,$\left\{\begin{array}{l} ∠EBC=∠FDC,\\ ∠BEC=∠DFC,\\ BC=DC,\end{array}\right. $$\therefore \triangle CBE\cong \triangle CDF(AAS),$$\therefore FC=EC$,
∴点C在$∠DAB$的平分线上.

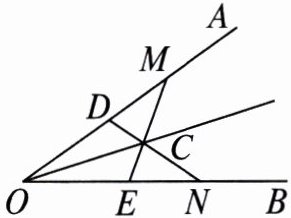
6. 如图,在 $ \angle AOB $ 的两边 $ OA $,$ OB $ 上分别取 $ OM = ON $,$ OD = OE $,$ DN $ 和 $ EM $ 相交于点 $ C $. 求证：点 $ C $ 在 $ \angle AOB $ 的平分线上.

答案：
证明 过点C作$CG⊥OA$于点G,$CF⊥OB$于点F,如图,在$\triangle MOE$和$\triangle NOD$中,$\left\{\begin{array}{l} OM=ON,\\ ∠MOE=∠NOD,\\ OE=OD,\end{array}\right. $$\therefore \triangle MOE\cong \triangle NOD(SAS),\therefore S_{\triangle MOE}=S_{\triangle NOD},$即$S_{\triangle MDC}=S_{\triangle NEC}.$$\because OM=ON,OD=OE,\therefore MD=NE,$$\therefore CG=CF.$$\because CG⊥OA,CF⊥OB$,
∴点C在$∠AOB$的平分线上.