《2025年同步测控优化设计八年级数学上册人教版福建专版》

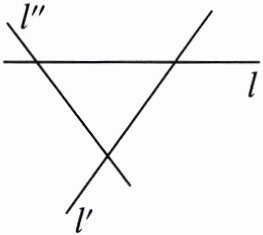
5. 如图,直线l,l',l''分别表示三条相互交叉的公路,现计划建一个加油站,要求加油站到这三条公路的距离相等,则可供选择的地址有( )


A.一处
B.二处
C.三处
D.四处

答案： D

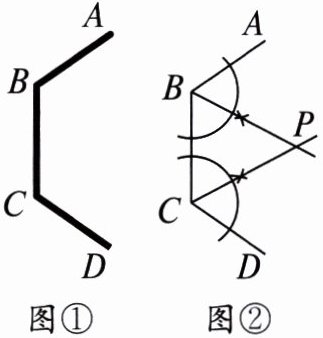
6. 校园一角的形状如图①,其中AB,BC,CD表示围墙.小亮通过作角平分线在图示的区域中找到了一点P(如图②),使得点P到三面墙的距离都相等.你能解释他这样做的道理吗？

答案：
解 如图,过点P作$PE\perp AB$于点E,$PF\perp BC$于点F,$PG\perp CD$于点G,$\because BP,CP$分别是$\angle ABC,\angle BCD$ 的平分线，$\therefore PE=PF,PF=PG,$$\therefore PE=PF=PG$.故点P到三面墙的距离都相等.

角的平分线的判定
(1)角的内部到角两边距离相等的点在______上.
(2)三角形的三条角平分线交于______,这一点到三角形三边的距离______.

答案：
(1)角的平分线　
(2)一点　相等

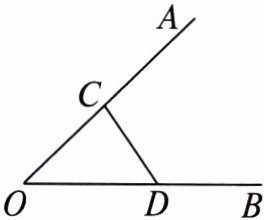
1. 如图,在 $ CD $ 上作一点 $ P $,使它到 $ OA $,$ OB $ 的距离相等,则点 $ P $ 是( )


A.线段 $ CD $ 的中点
B.$ \triangle OCD $ 的边 $ CD $ 上的高与 $ CD $ 的交点
C.$ CD $ 与 $ \angle AOB $ 的平分线的交点
D.以上答案都不对

答案： C

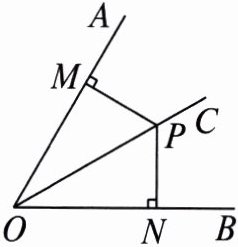
2. 如图,$ PM = PN $,$ \angle BOC = 30^{\circ} $,则 $ \angle AOB = $______.

答案： $60^{\circ }$