1. 作已知角的平分线
已知∠AOB,求作∠AOB的平分线。

作法:如图,已知∠AOB。
(1)以点O为圆心,适当长为半径作弧,交OA于点M,交OB于点N。
(2)分别以点M,N为圆心,____的长为半径作弧,两弧在∠AOB的____相交于点C。
(3)作射线OC.射线OC即为∠AOB的平分线。
已知∠AOB,求作∠AOB的平分线。

作法:如图,已知∠AOB。
(1)以点O为圆心,适当长为半径作弧,交OA于点M,交OB于点N。
(2)分别以点M,N为圆心,____的长为半径作弧,两弧在∠AOB的____相交于点C。
(3)作射线OC.射线OC即为∠AOB的平分线。
答案:
大于$\frac{1}{2}MN$ 内部
2. 角的平分线的性质
角的平分线上的点到角两边的距离____。
角的平分线上的点到角两边的距离____。
答案:
相等
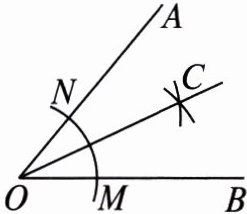
1. 如图,用直尺和圆规作一个角的平分线,能说明∠AOC= ∠BOC的依据是( )
A.SAS
B.ASA
C.SSS
D.AAS

A.SAS
B.ASA
C.SSS
D.AAS
答案:
C
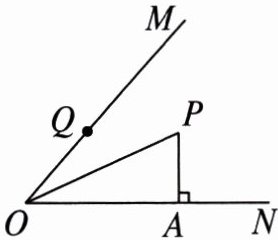
2. 如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA= 3,则PQ的最小值为( )
A.1
B.2
C.3
D.4

A.1
B.2
C.3
D.4
答案:
C
3. 如图,在△ABC中,AD平分∠BAC,DE⊥AB于点E,△ABC的面积为7,AB= 4,DE= 2,则AC的长是____。


答案:
3
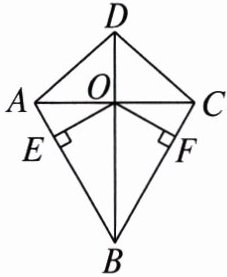
4. 我们把两组邻边相等的四边形叫作“筝形”,如图,四边形ABCD是一个筝形,其中AB= CB,AD= CD,对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E,F.求证OE= OF。

答案:
证明 在$\triangle ABD$和$\triangle CBD$中,$\left\{\begin{array}{l} AB=CB,\\ AD=CD,\\ BD=BD,\end{array}\right. $$\therefore \triangle ABD\cong \triangle CBD(SSS),\therefore \angle ABD=\angle CBD,$$\therefore BD$平分$\angle ABC.$$\because OE\perp AB,OF\perp CB,\therefore OE=OF.$
查看更多完整答案,请扫码查看


