《2025年同步测控优化设计八年级数学上册人教版福建专版》

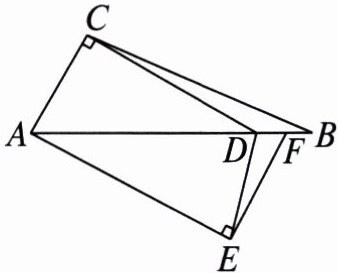
4. 如图,点 $ D $,$ F $ 在线段 $ AB $ 上,$ \angle ACD = 90^{\circ} $,$ \angle AEF = 90^{\circ} $,且 $ \angle ADE $ 是锐角,写出图中的锐角三角形、直角三角形和钝角三角形.

答案： 解 锐角三角形为△AED，直角三角形为△ACD，△AEF，钝角三角形为△ABC，△BDC，△DEF.

5. 若 $ \triangle ABC $ 三条边的长度分别为 $ m $,$ n $,$ p $,且 $ |m - n| + (n - p)^2 = 0 $,则 $ \triangle ABC $ 为( )

A.等腰三角形
B.等边三角形
C.直角三角形
D.钝角三角形

答案： B

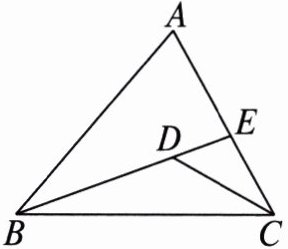
6. 假定有一条公共边的两个三角形称为一对“共边三角形”,则图中以 $ BC $ 为公共边的“共边三角形”有______对.

答案： 3

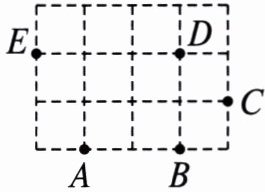
7. 如图,以 $ A $,$ B $,$ C $,$ D $,$ E $ 五个点中的任意三个点为顶点画三角形.
(1)一共可以画出几个三角形？用符号表示这些三角形.
(2)以 $ AB $ 为一边可以画出哪几个三角形？以 $ C $ 为顶点可以画出哪几个三角形？
(3)从画出的三角形中分别找出 1 个直角三角形和 1 个钝角三角形.

答案： 解
(1)10 个，△ABC，△ABD，△ABE，△ACD，△ACE，△ADE，△BCD，△BCE，△BDE，△CDE.
(2)以 AB 为一边的三角形有△ABC，△ABD，△ABE；以 C 为顶点的三角形有△ABC，△ACD，△ACE，△BCD，△BCE，△CDE.
(3)找出的三角形分别为△ABD，△ABC.(答案不唯一)

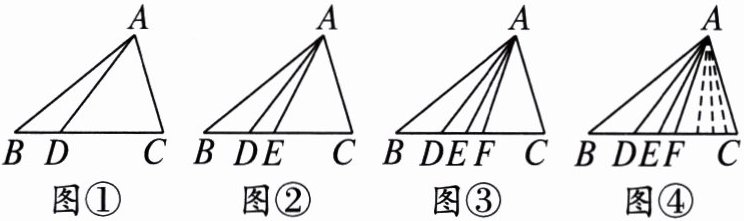
8. 已知 $ \triangle ABC $.
(1)如图①,在边 $ BC $ 上取一个点 $ D $,连接 $ AD $,则图中共有多少个三角形？
(2)如图②,在边 $ BC $ 上取两个点 $ D $,$ E $,连接 $ AD $,$ AE $,则图中共有多少个三角形？
(3)如图③,在边 $ BC $ 上取三个点 $ D $,$ E $,$ F $,连接 $ AD $,$ AE $,$ AF $,则图中共有多少个三角形？
(4)如图④,在边 $ BC $ 上取 $ n $ 个点 $ D $,$ E $,$ F $,…$$,连接 $ AD $,$ AE $,$ AF $,…$$,则图中共有多少个三角形？

答案： 解
(1)2+1=3(个).
(2)3+2+1=6(个).
(3)4+3+2+1=10(个).
(4)由前 3 问可推导得(n+1)+n+(n-1)+…+1=$\frac{[(n+1)+1](n+1)}{2}$=$\frac{(n+2)(n+1)}{2}$(个).