4. 如图,$OA = OB$,$AC = BC$. 求证$∠AOC = ∠BOC$.


答案:
证明
∵在△OAC和△OBC中,{OA=OB,OC=OC,AC=BC,
∴△OAC≌△OBC(SSS),
∴∠AOC=∠BOC.
∵在△OAC和△OBC中,{OA=OB,OC=OC,AC=BC,
∴△OAC≌△OBC(SSS),
∴∠AOC=∠BOC.
5. 如图,点$A$,$D$,$C$,$B$在同一条直线上,$AD = BC$,$AE = BF$,$CE = DF$,求证$AE// BF$.


答案:
证明
∵AD=BC,
∴AC=BD.
在△ACE和△BDF中,{AC=BD,AE=BF,CE=DF,
∴△ACE≌△BDF(SSS),
∴∠A=∠B,
∴AE//BF.
∵AD=BC,
∴AC=BD.
在△ACE和△BDF中,{AC=BD,AE=BF,CE=DF,
∴△ACE≌△BDF(SSS),
∴∠A=∠B,
∴AE//BF.
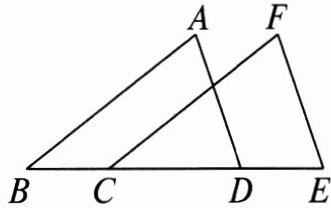
6. 如图,点$B$,$C$,$D$,$E$在同一条直线上,$AB = FC$,$AD = FE$,$BC = DE$,探索$AB与FC$的位置关系,并说明理由.

答案:
解 AB//FC.
理由:
∵BC=DE,
∴BC+CD=DE+CD,
即BD=CE.
在△ABD和△FCE中,{BD=CE,AD=FE,AB=FC,
∴△ABD≌△FCE(SSS),
∴∠B=∠FCE,
∴AB//FC.
理由:
∵BC=DE,
∴BC+CD=DE+CD,
即BD=CE.
在△ABD和△FCE中,{BD=CE,AD=FE,AB=FC,
∴△ABD≌△FCE(SSS),
∴∠B=∠FCE,
∴AB//FC.
7. 如图,在四边形$ABCD$中,$E是BC$的中点,连接$AC$,$AE$,若$AB = AC$,$AE = CD$,$AD = CE$,图中的全等三角形有几对?请分别证明它们.


答案:
解 三对.
证明:
在△ABE和△ACE中,{AB=AC,AE=AE,BE=CE,
∴△ABE≌△ACE(SSS).
在△AEC和△CDA中,{AE=CD,AC=AC,EC=DA,
∴△AEC≌△CDA(SSS).
∴△ABE≌△CAD.
证明:
在△ABE和△ACE中,{AB=AC,AE=AE,BE=CE,
∴△ABE≌△ACE(SSS).
在△AEC和△CDA中,{AE=CD,AC=AC,EC=DA,
∴△AEC≌△CDA(SSS).
∴△ABE≌△CAD.
查看更多完整答案,请扫码查看


