《2025年同步测控优化设计八年级数学上册人教版福建专版》

5. 如图,$△ACE≌△DBF$,$CE= BF$,$AE= DF$,$AD= 8$,$BC= 2$.
(1)求$AC$的长度；
(2)试说明$CE// BF$.

答案：
(1)
∵△ACE≌△DBF，
∴AC=BD，即AB=DC.
∵BC=2，
∴2AB+2=8，
解得AB=3，故AC=3+2=5.
(2)
∵△ACE≌△DBF，
∴∠ECA=∠FBD，
∴CE//BF.

6. 如图,点$B$,$C$,$D$在同一条直线上,$△ABC≌△CDE$,$∠B= ∠D= 90^{\circ}$,$AB= 6$,$BC= 8$,$CE= 10$.
(1)求$△ABC$的周长；
(2)求$△ACE$的面积.

答案：
(1)
∵△ABC≌△CDE，CE=10，
∴AC=CE=10.
∵AB=6，BC=8，
∴△ABC的周长为AB+BC+AC=6+8+10=24.
(2)
∵∠B=90°，
∴∠ACB+∠BAC=90°.
∵△ABC≌△CDE，
∴∠ECD=∠CAB，
∴∠ACB+∠ECD=90°，
∴∠ACE=90°.
∵AC=CE=10，
∴△ACE的面积为$\frac{1}{2}$AC·CE=$\frac{1}{2}$×10×10=50.

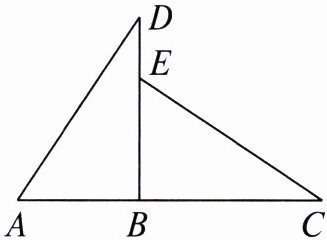
7. 如图,点$A$,$B$,$C$在同一直线上,$△ABD≌△EBC$,点$E在BD$上,$AB= 2\ cm$,$BC= 3\ cm$.
(1)求$DE$的长；
(2)判断$DB与AC$的位置关系,并说明理由；
(3)判断直线$AD与直线CE$的位置关系,并说明理由.

答案：

(1)
∵△ABD≌△EBC，
∴BD=BC=3 cm，BE=AB=2 cm，
∴DE=BD-BE=1 cm.
(2)DB与AC垂直.
理由：
∵△ABD≌△EBC，
∴∠ABD=∠EBC，且A，B，C在一条直线上，
∴∠ABD=∠EBC=90°，
∴DB与AC垂直.
(3)直线AD与直线CE垂直.
理由：如图，延长CE交AD于点F，

∵△ABD≌△EBC，
∴∠D=∠C.
∵由
(2)知，∠A +∠D=90°，
∴∠A+∠C=90°，
∴∠AFC=90°，
即CE⊥AD.