《2025年同步测控优化设计八年级数学上册人教版福建专版》

1. 全等形的概念
能够____的两个图形叫作全等形.

答案： 完全重合

2. 全等三角形及有关概念
(1)能够____的两个三角形叫作全等三角形.
(2)把两个全等的三角形重合到一起,重合的顶点叫作____,重合的边叫作____,重合的角叫作____.
(3)“全等”用符号“____”表示,读作“全等于”；记两个三角形全等时,通常把表示对应顶点的字母写在____的位置上.

答案：
(1)完全重合
(2)对应顶点 对应边 对应角
(3)≌ 对应

3. 全等三角形的性质
全等三角形的对应边____,全等三角形的对应角____.

答案： 相等 相等

1. 下列各组图形中,属于全等形的是( )

答案： C

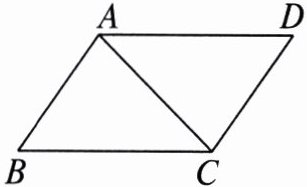
2. 如图,$△ABC≌△CDA$,$∠BAC= ∠DCA$,$∠B= ∠D$,对于以下结论：
①$AB与CD$是对应边；②$AC与CA$是对应边；③点$A与点A$是对应顶点；④点$C与点C$是对应顶点；⑤$∠ACB与∠CAD$是对应角. 其中正确的有( )


A.2个
B.3个
C.4个
D.5个

答案： B

3. 如图,$△ABC≌△A_1B_1C_1$,$∠A= 110^{\circ}$,$∠B= 40^{\circ}$,可得$∠C_1= $____.

答案： 30°

4. 如图,$△ABE≌△ACD$.
(1)如果$BE= 6$,$DE= 2$,求$BC$的长；
(2)如果$∠BAC= 75^{\circ}$,$∠BAD= 30^{\circ}$,求$∠DAE$的度数.

答案：
(1)
∵△ABE≌△ACD，
∴CD=BE=6.
∴CE=CD-DE=6-2=4.
∴BC=BE+CE=6+4=10.
(2)
∵△ABE≌△ACD，
∴∠BAE=∠CAD，
∴∠BAE-∠DAE=∠CAD-∠DAE，
即∠BAD=∠CAE=30°，
∴∠DAE=∠BAC-∠BAD-∠CAE=75°-30°-30°=15°.