《2025年同步测控优化设计八年级数学上册人教版福建专版》

1. 三角形外角的概念
三角形的一边与另一边的____组成的角,叫作三角形的外角.

答案： 延长线

2. 三角形外角的推论
三角形的外角等于与它____的两个内角的和.

答案： 不相邻

1. 如图,在下列选项中,是$\triangle ABC$的外角的是( )


A.$\angle 1$
B.$\angle 2$
C.$\angle 3$
D.$\angle 4$

答案： C

2. 如图,$\angle ACD = 120^{\circ}$,$\angle B = 20^{\circ}$,则$\angle A$的度数是( )


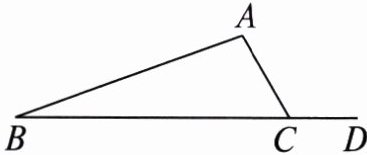
A.$120^{\circ}$
B.$90^{\circ}$
C.$100^{\circ}$
D.$30^{\circ}$

答案： C

3. 如图,小明同学在“三角尺拼角”实验中把一副三角尺按图中的方式放置,则$\angle 1= $____.

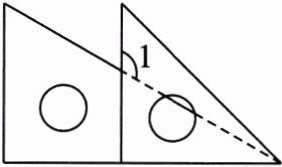
答案： 120°

4. 求图中的$x$.

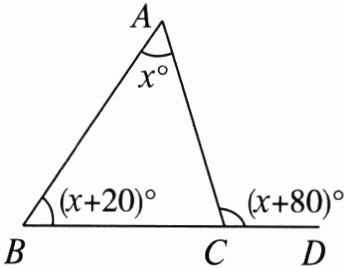
答案： 解
∵∠ACD是△ABC的外角，
∴∠ACD=∠A+∠B，
即(x+80)°=x°+(x+20)°，解得x=60.

5. 如图,在$\triangle ABC$中,$\angle 1 = \angle 2 = \angle 3$.
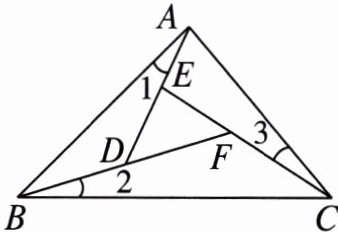
(1)求证$\angle ABC = \angle EDF$.
(2)若$\angle ABC = 45^{\circ}$,$\angle DFE = 50^{\circ}$,求$\angle BAC$的度数.

答案：
(1)证明
∵∠EDF是△ABD的一个外角，
∴∠EDF=∠1+∠ABD.
∵∠1=∠2，
∴∠EDF=∠2+∠ABD=∠ABC，
即∠ABC=∠EDF.
(2)解
∵∠DEF是△ACE的一个外角，
∴∠DEF=∠3+∠CAE.
∵∠1=∠3，
∴∠DEF=∠1+∠CAE=∠BAC.
由
(1)得∠EDF=∠ABC=45°，
∵∠DFE=50°，
∴∠DEF=180°-∠EDF-∠DFE=85°，即∠BAC=85°.

6. 如图,$AC$,$BD相交于点O$,$BE$,$CE分别平分\angle ABD$,$\angle ACD$,$\angle A = 50^{\circ}$,$\angle D = 44^{\circ}$,求$\angle E$的度数.

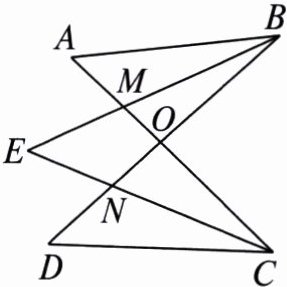
答案： 解
∵∠BNC=∠D+∠DCN，∠BNC=∠E+∠EBN，
∴∠D+∠DCN=∠E+∠EBN.
同理，∠A+∠ABE=∠E+∠ACE，
∴∠D+∠DCN+∠A+∠ABE=2∠E+∠EBN+∠ACE.
∵BE，CE分别平分∠ABD，∠ACD，
∴∠DCN=∠ACE，∠ABE=∠EBN，
∴∠D+∠A=2∠E.
∵∠A=50°，∠D=44°，
∴∠E=47°.