第88页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
1. 如图24-2-4-3,PA,PB是⊙O的切线,A,B为切点,AC是⊙O的直径,∠BAC= 20°,求∠P的度数为(
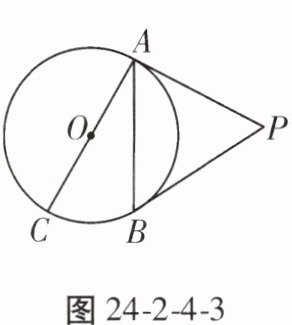
A.$50^{\circ}$
B.$70^{\circ}$
C.$110^{\circ}$
D.$40^{\circ}$
D
)
A.$50^{\circ}$
B.$70^{\circ}$
C.$110^{\circ}$
D.$40^{\circ}$
答案:
D
2. 如图24-2-4-4,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切,切点分别是D,C,E。若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是(
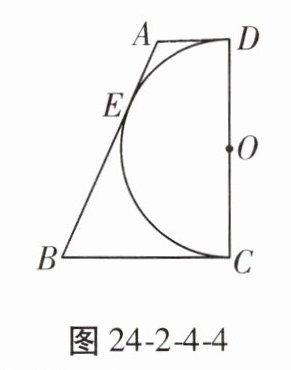
A.9
B.10
C.12
D.14
D
)
A.9
B.10
C.12
D.14
答案:
D
3. (2021临沂中考)如图24-2-4-5,PA,PB分别与⊙O相切于A,B两点,∠P= 70°,C为⊙O上一点,则∠ACB的度数为(
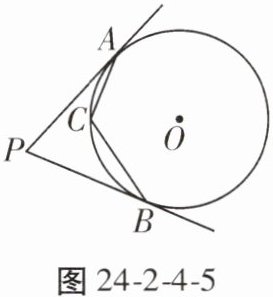
A.$110^{\circ}$
B.$120^{\circ}$
C.$125^{\circ}$
D.$130^{\circ}$
C
)
A.$110^{\circ}$
B.$120^{\circ}$
C.$125^{\circ}$
D.$130^{\circ}$
答案:
C
4. 如图24-2-4-6,点O是△ABC的内心,过点O作EF//AB,与AC,BC分别交于点E,F,则(
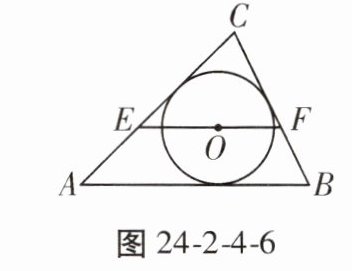
A.EF$>$AE+BF
B.EF$<$AE+BF
C.EF= AE+BF
D.EF$\leqslant$AE+BF
C
)
A.EF$>$AE+BF
B.EF$<$AE+BF
C.EF= AE+BF
D.EF$\leqslant$AE+BF
答案:
C
5. 《九章算术》是东方数学思想之源,该书中记载:“今有勾八步,股一十五步,问勾中容圆径几何。”其意思为:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形内切圆的直径是多少步。”该问题的答案是
6
步。
答案:
6
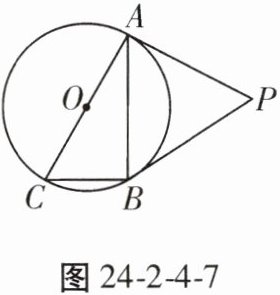
6. 如图24-2-4-7,⊙O是Rt△ABC的外接圆,∠ABC= 90°,点P是圆外一点,PA切⊙O于点A,且PA= PB。
(1)求证:PB是⊙O的切线;
(2)已知PA= $\sqrt{3}$,∠ACB= 60°,求⊙O的半径。
(1)求证:PB是⊙O的切线;
(2)已知PA= $\sqrt{3}$,∠ACB= 60°,求⊙O的半径。

答案:
1. (1)证明:
连接$OB$。
因为$OA = OB$,所以$\angle OAB=\angle OBA$。
因为$PA = PB$,所以$\angle PAB=\angle PBA$。
所以$\angle OAB+\angle PAB=\angle OBA+\angle PBA$,即$\angle PAO=\angle PBO$。
因为$PA$切$\odot O$于点$A$,所以$OA\perp PA$,即$\angle PAO = 90^{\circ}$。
所以$\angle PBO=\angle PAO = 90^{\circ}$,$OB\perp PB$。
又因为$OB$是$\odot O$的半径,所以$PB$是$\odot O$的切线。
2. (2)解:
因为$\angle ABC = 90^{\circ}$,所以$AC$是$\odot O$的直径。
因为$\angle ACB = 60^{\circ}$,所以$\angle BAC = 30^{\circ}$。
设$\odot O$的半径为$r$,则$AC = 2r$,$AB=\sqrt{3}r$。
由(1)知$PA = PB$,$OA\perp PA$,$OB\perp PB$,又$OA = OB$,$OP = OP$,所以$\triangle AOP\cong\triangle BOP(HL)$,则$\angle APO=\angle BPO$。
因为$\angle APB + \angle PAB+\angle PBA=180^{\circ}$,$\angle PAB=\angle PBA$,$\angle OAB=\angle OBA$,$\angle OAB+\angle PAB = 90^{\circ}$,所以$\angle APB = 60^{\circ}$。
又因为$PA = PB$,所以$\triangle PAB$是等边三角形。
所以$PA = AB$。
已知$PA=\sqrt{3}$,则$\sqrt{3}r=\sqrt{3}$。
解得$r = 1$。
所以$\odot O$的半径为$1$。
连接$OB$。
因为$OA = OB$,所以$\angle OAB=\angle OBA$。
因为$PA = PB$,所以$\angle PAB=\angle PBA$。
所以$\angle OAB+\angle PAB=\angle OBA+\angle PBA$,即$\angle PAO=\angle PBO$。
因为$PA$切$\odot O$于点$A$,所以$OA\perp PA$,即$\angle PAO = 90^{\circ}$。
所以$\angle PBO=\angle PAO = 90^{\circ}$,$OB\perp PB$。
又因为$OB$是$\odot O$的半径,所以$PB$是$\odot O$的切线。
2. (2)解:
因为$\angle ABC = 90^{\circ}$,所以$AC$是$\odot O$的直径。
因为$\angle ACB = 60^{\circ}$,所以$\angle BAC = 30^{\circ}$。
设$\odot O$的半径为$r$,则$AC = 2r$,$AB=\sqrt{3}r$。
由(1)知$PA = PB$,$OA\perp PA$,$OB\perp PB$,又$OA = OB$,$OP = OP$,所以$\triangle AOP\cong\triangle BOP(HL)$,则$\angle APO=\angle BPO$。
因为$\angle APB + \angle PAB+\angle PBA=180^{\circ}$,$\angle PAB=\angle PBA$,$\angle OAB=\angle OBA$,$\angle OAB+\angle PAB = 90^{\circ}$,所以$\angle APB = 60^{\circ}$。
又因为$PA = PB$,所以$\triangle PAB$是等边三角形。
所以$PA = AB$。
已知$PA=\sqrt{3}$,则$\sqrt{3}r=\sqrt{3}$。
解得$r = 1$。
所以$\odot O$的半径为$1$。
7. 如图24-2-4-8,在半径为5的⊙O中,将劣弧AB沿弦AB翻折,使折叠后的$\overset{\frown}{AB}$恰好与OA,OB相切,则弦AB的长为(
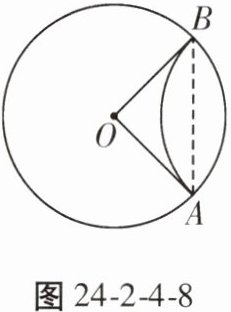
A.5
B.$5\sqrt{2}$
C.10
D.$10\sqrt{2}$
B
)
A.5
B.$5\sqrt{2}$
C.10
D.$10\sqrt{2}$
答案:
B
查看更多完整答案,请扫码查看


