《2025年绩优学案九年级数学上册人教版》

【例1】如图24-2-3-2,AB是⊙O的直径,C是⊙O上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC= ∠CAD。求证：直线MN是⊙O的切线。

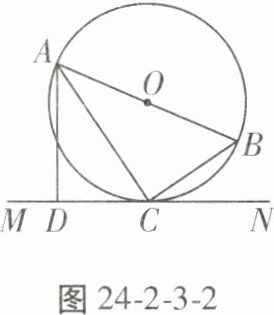
解题关键 连接OC,推出AD//OC,根据切线的判定推出OC⊥MN即可。

答案： 证明:连接OC。
∵ OA = OC,
∴ ∠BAC = ∠ACO。
∵ ∠BAC = ∠CAD,
∴ ∠ACO = ∠CAD,
∴ OC//AD。又 AD⊥MN,
∴ OC⊥MN,
∴ 直线 MN 是⊙O 的切线。

【例2】如图24-2-3-3,AC是⊙O的直径,AB是⊙O的一条弦,AP是⊙O的切线。作BM= AB并与AP交于点M,延长MB交AC于点E,交⊙O于点D,连接AD。求证：AB= BE。

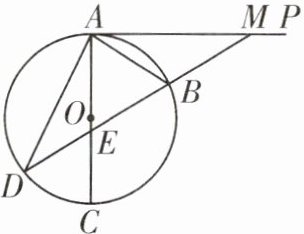
解题关键 根据切线的性质得出∠EAM= 90°,利用等腰三角形的性质与余角的性质解决问题。

答案： 证明:
∵ AP 是⊙O 的切线,
∴ ∠EAM = 90°,
∴ ∠BAE + ∠MAB = 90°,∠AEB + ∠AMB = 90°。又 AB = BM,
∴ ∠MAB = ∠AMB,
∴ ∠BAE = ∠AEB,
∴ AB = BE。