《2025年绩优学案九年级数学上册人教版》

【例2】如图24-2-1-3,在$\triangle ABC$中,$AB= AC= 10$,$BC= 12$,求$\triangle ABC$外接圆的半径。

解题关键 通过作辅助线$AD\perp BC$,结合垂径定理,可将求半径问题转化为求直角三角形的斜边长。

答案：
解:如图,过点A作AD⊥BC,垂足为D。
∵AB=AC,
∴AD垂直平分BC,且外心O在AD上。
　　　　　　　　　　　
∴BD=1/2BC=6。
　在Rt△BDA中,AD= √(AB²−BD²)=√(10²−6²)=8。
　连接OC,设OA=OC=r,则OD=8−r,即(8−r)²+6²=r²,解得r=25/4,即△ABC外接圆的半径为25/4。

【例3】若用反证法证明命题“四边形中至少有一个角是钝角或直角”时,则首先应该假设这个四边形中 (C)
A.至少有一个角是钝角或直角
B.没有一个角是锐角
C.没有一个角是钝角或直角
D.每一个角都是钝角或直角
解题关键 反证法中的假设必须与原命题的结论相反,本题中“至少”的相对面是“不存在”。
知识延伸
用反证法证明命题时,假设必须合理、全面,要注意命题结论的“反面”是一种情形还是多种情形,做到假设“不重复、不遗漏”。

答案： C

1. 已知$\odot O的直径为10cm$,点$P不在\odot O$外,则$OP$的长 (B)
A.小于$5cm$
B.不大于$5cm$
C.小于$10cm$
D.不大于$10cm$

答案： B

2. 小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图24-2-1-4所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是 (B)

A.第①块
B.第②块
C.第③块
D.第④块

答案： B

3. 用反证法证明“同一平面内,若$a\perp c$,$b\perp c$,则$a// b$”时,应假设 (D)
A.$a不垂直于c$
B.$a$,$b都不垂直于c$
C.$a\perp b$
D.$a与b$相交

答案： D

4. 平面直角坐标系内的三个点$A(1,-3)$,$B(0,-3)$,$C(2,-3)$,$\underset{\sim}{}$不能确定一个圆。(填“能”或“不能”)

答案： 不能

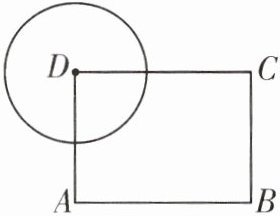
5. 如图24-2-1-5,在矩形$ABCD$中,$AB= 4$,$AD= 3$,以顶点$D为圆心作半径为r$的圆,若要使另外三个顶点$A$,$B$,$C$中至少有一个点在圆内,且至少有一个点在圆外,则$r的取值范围是\underset{\sim}{}$3＜r＜5。

答案： 3＜r＜5