《2025年绩优学案九年级数学上册人教版》

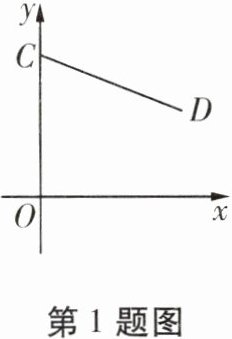
1. 如图的直角坐标系中,点C,D的坐标分别为$(0,10)$,$(10,6)$,连接CD,以C为中心,将线段CD旋转$90^{\circ}$,则旋转后点D的对应点$D'$的坐标是(4,20)或(-4,0)。

答案： (4,20)或(-4,0)

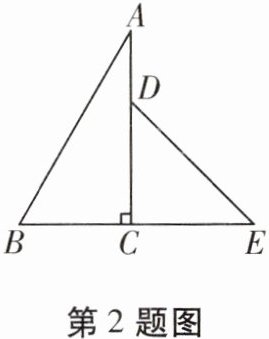
2. 如图,$Rt\triangle ABC和Rt\triangle DCE$中,$\angle ACB= \angle DCE= 90^{\circ}$,$\angle A= 30^{\circ}$,$\angle E= 45^{\circ}$,B,C,E三点共线,$Rt\triangle ABC$不动,将$\triangle DCE$绕点C逆时针旋转$\alpha(0^{\circ}＜\alpha＜360^{\circ})$,当$DE// BC$时,$\alpha=$45°或225°。

答案： 45°或225°

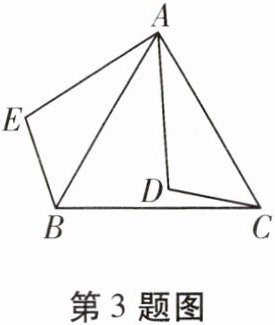
3. 如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转$60^{\circ}$,得到线段AE,连接CD,BE。
(1)求证：$\angle AEB= \angle ADC$；
(2)连接DE,若$\angle ADC= 105^{\circ}$,求$\angle BED$的度数。

答案：
(1)略　
(2)∠BED=45°

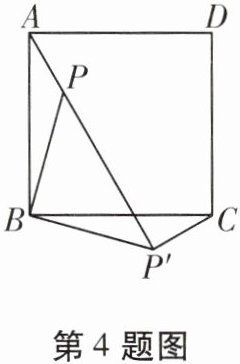
4. 如图,四边形ABCD是正方形,P是正方形内任意一点,连接PA,PB,将$\triangle PAB$绕点B顺时针旋转至$\triangle P'CB$处,连接$PP'$。
(1)猜想$\triangle PBP'$的形状,并说明理由；
(2)若$PP'= 2\sqrt{2}cm$,求$S_{\triangle PBP'}$。

答案： 解:
(1)△PBP'是等腰直角三角形
(2)
∵PP'=2√2cm,
∴点B到PP'的距离=1/2PP'=√2cm,
∴S△PBP'=1/2×2√2×√2=2(cm²)。

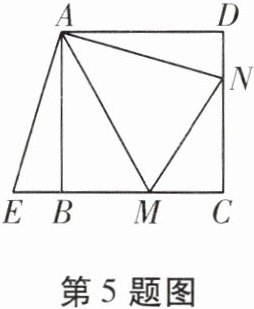
5. 如图,点M,N分别在正方形ABCD的边BC,CD上,且$\angle MAN= 45^{\circ}$。把$\triangle ADN$绕点A顺时针旋转$90^{\circ}得到\triangle ABE$。
(1)求证：$\triangle AEM\cong\triangle ANM$；
(2)若$BM= 3$,$DN= 2$,求正方形ABCD的边长。

答案： 1. （1）证明：
因为$\triangle ADN$绕点$A$顺时针旋转$90^{\circ}$得到$\triangle ABE$，
所以$\triangle ADN\cong\triangle ABE$，则$AN = AE$，$\angle DAN=\angle BAE$。
因为四边形$ABCD$是正方形，所以$\angle BAD = 90^{\circ}$，又$\angle MAN = 45^{\circ}$，那么$\angle BAM+\angle DAN=\angle BAD-\angle MAN = 90^{\circ}-45^{\circ}=45^{\circ}$。
把$\angle DAN=\angle BAE$代入上式得：$\angle BAM+\angle BAE = 45^{\circ}$，即$\angle EAM = 45^{\circ}$。
在$\triangle AEM$和$\triangle ANM$中：
$AE = AN$（已证），$\angle EAM=\angle NAM = 45^{\circ}$，$AM = AM$（公共边）。
根据$SAS$（边角边）定理，可得$\triangle AEM\cong\triangle ANM$。
2. （2）解：
设正方形$ABCD$的边长为$x$。
因为$\triangle AEM\cong\triangle ANM$，所以$EM = MN$。
由$\triangle ADN\cong\triangle ABE$可知$BE = DN = 2$。
又$BM = 3$，所以$EM=BE + BM=2 + 3 = 5$，则$MN = 5$。
因为$MC=x - 3$，$NC=x - 2$。
在$Rt\triangle MNC$中，根据勾股定理$MN^{2}=MC^{2}+NC^{2}$，即$5^{2}=(x - 3)^{2}+(x - 2)^{2}$。
展开得$25=x^{2}-6x + 9+x^{2}-4x + 4$。
整理得$2x^{2}-10x+13 - 25 = 0$，即$2x^{2}-10x - 12 = 0$，两边同时除以$2$得$x^{2}-5x - 6 = 0$。
分解因式得$(x - 6)(x + 1)=0$。
则$x - 6 = 0$或$x + 1 = 0$，解得$x = 6$或$x=-1$（边长不能为负舍去）。
所以正方形$ABCD$的边长为$6$。