《2025年绩优学案九年级数学上册人教版》

7. 某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图22-3-1-2所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,则能建成的饲养室面积最大为 (A)

$A.75 m^2$
B.$\frac{75}{2}$ m^2
$C.48 m^2$
D.$\frac{225}{2}$ m^2

答案： A

8. 工人师傅用一块长为12 dm,宽为8 dm的矩形铁皮制作一个无盖长方体容器,需要将四角各裁掉一个正方形(厚度不计)。
(1)请在图中画出裁剪示意图,用实线表示裁剪线,用虚线表示折痕；
(2)若要求制作的长方体的底面长不大于底面宽的5倍(长大于宽),并将容器外表面进行防锈处理,侧面每平方分米的费用为0.5元,底面每平方分米的费用为2元,裁掉的正方形的边长为多少时,总费用最低？最低费用为多少元？

答案： 解:
(1)略
(2)设总费用为y元,裁样的正方形的边长为x dm,则y=2(12-2x)(8-2x)+0.5×[2x(12-2x)+2x(8-2x)]=4x²-60x+192=4(x-7.5)²-33,又
∵12-2x≤5(8-2x),
∴x≤3.5,
∵a=4＞0,
∴x＜7.5时,y随x的增大而减小,
∴当x=3.5时,y取得最小值,最小值为31。

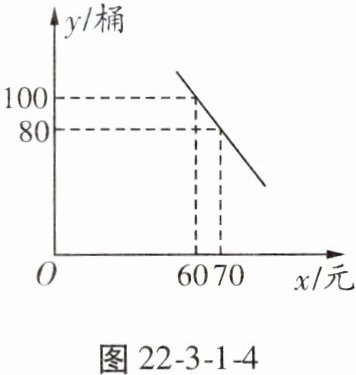
9. 某药店新进一批桶装消毒液,每桶进价50元,每天的销售量y(桶)与销售单价x(元)之间满足一次函数关系,其图象如图22-3-1-4所示。
(1)求y与x之间的函数表达式；
(2)每桶消毒液的销售单价定为多少元时,药店每天获得的利润最大？最大利润是多少元？(单件利润= 销售单价-进价)

答案： 解:
(1)y=-2x+220
(2)设药店每天获得的利润为w元,由题意,得w=(x-50)(-2x+220)=-2(x-80)²+1800,
∵-2＜0,函数有最大值,
∴当x=80时,w有最大值,此时最大值是1800。故销售单价定为80元时,该药店每天获得的利润最大,最大利润是1800元。

10. (动点问题)如图22-3-1-5,已知抛物线经过A(-3,0),B(0,3)两点,且其对称轴为直线x= -1。
(1)求此抛物线的解析式；
(2)若点P是抛物线上点A与点B之间的动点(不包括点A,B),求△PAB的面积的最大值,并求出此时点P的坐标。

答案： 解:
(1)y=-x²-2x+3
(2)设直线AB的解析式为y=kx+b,
∵A(-3,0),B(0,3),
∴{-3k+b=0,b=3,解得{k=1,b=3。
∴直线AB的解析式为y=x+3,作PQ⊥x轴,垂足为点Q,交直线AB于点M,设P(x,-x²-2x+3),则M(x,x+3),
∴PM=-x²-2x+3-(x+3)=-x²-3x,
∴S△PAB=1/2(-x²-3x)×3=-3/2(x+3/2)²+27/8,当x=-3/2时,S△PAB最大=27/8,y=-(-3/2)²-2×(-3/2)+3=15/4,
∴△PAB的面积的最大值为27/8,此时点P的坐标为(-3/2,15/4)。