《2025年绩优学案九年级数学上册人教版》

1. 下列函数中,是二次函数的是(B)
A.$ y = ax^{2} + bx + c $
B.$ y = x(2x - 3) $
C.$ y = (x + 4)^{2} - x^{2} $
D.$ y = \frac{1}{x^{2}} $

答案： B

2. 关于函数 $ y = (500 - 10x)(40 + x) $,下列说法不正确的是(C)
A.$ y $ 是 $ x $ 的二次函数
B.二次项系数是 $ - 10 $
C.一次项是 $ - 100 $
D.常数项是 $ 20000 $

答案： C

3. 设 $ 160 $ 元的电器连续两次降价后的价格为 $ y $ 元,若平均每次降价的百分率是 $ x $,则 $ y $ 与 $ x $ 的函数关系式为(D)
A.$ y = 320(x - 1) $
B.$ y = 320(1 - x) $
C.$ y = 160(1 - x^{2}) $
D.$ y = 160(1 - x)^{2} $

答案： D

4. 如果函数 $ y = (m - 1)x^{2} + x $($ m $ 是常数)是二次函数,那么 $ m $ 的取值范围是$m\neq 1$。

答案： $m\neq 1$

5. 下列函数中：① $ y = - x^{2} $；② $ y = 2x $；③ $ y = 22 + x^{2} - x^{3} $；④ $ m = 3 - t - t^{2} $(其中 $ x $,$ t $ 为自变量),二次函数有①④。(填序号)

答案： ①④

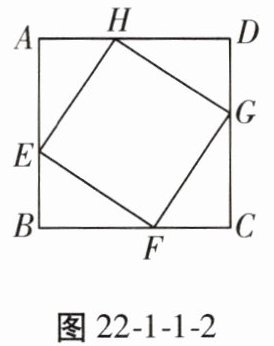
6. 如图 22 - 1 - 1 - 2,正方形 $ EFGH $ 的顶点在边长为 $ 2 $ 的正方形的边上。若设 $ AE = x $,正方形 $ EFGH $ 的面积为 $ y $,则 $ y $ 与 $ x $ 的函数关系式为$y=2x^{2}-4x+4(0＜x＜2)$。

答案： $y=2x^{2}-4x+4(0＜x＜2)$

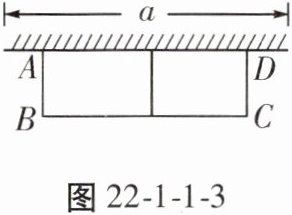
7. 如图 22 - 1 - 1 - 3,用长为 $ 24m $ 的篱笆,一面利用墙(墙的最大可用长度 $ a $ 为 $ 10m $)围成中间隔有一道篱笆的长方形花圃。设花圃的宽 $ AB $ 为 $ xm $,面积为 $ Sm^{2} $,则 $ S $ 与 $ x $ 的函数关系式为$S=-3x^{2}+24x$；自变量的取值范围为$\frac{14}{3}\leqslant x＜8$。

答案： $S=-3x^{2}+24x$ $\frac{14}{3}\leqslant x＜8$

8. 某商家销售具有地方特色的某种商品,每件进价为 $ 40 $ 元。经过市场调查,一周的销售量 $ y $(件)与销售单价 $ x(x \geqslant 50) $(元)的关系如下表：

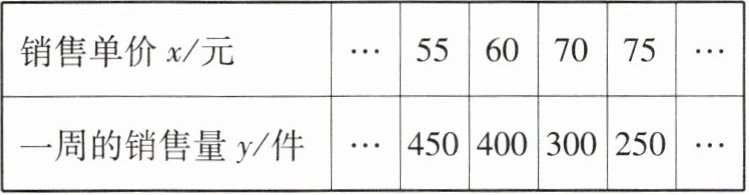
(1)直接写出 $ y $ 与 $ x $ 的函数关系式：$y=-10x+1000$；
(2)设一周的销售利润为 $ W $ 元,求出 $ W $ 与 $ x $ 的函数关系式。
由题意,得$W=(x-40)y=(x-40)(-10x+1000)=-10x^{2}+1400x-40000$。

答案： 解:
(1)$y=-10x+1000$
(2)由题意,得$W=(x-40)y=(x-40)(-10x+1000)=-10x^{2}+1400x-40000$。

9. 若函数 $ y = (a - 1)x^{b + 1} + x^{2} + 1 $ 是二次函数,试讨论 $ a $,$ b $ 的取值范围。

答案： 解:①$a-1+1\neq 0$且$b+1=2$,解得$b=1$且$a\neq 0$;②$a-1=0$且$b$为任意实数,解得$a=1$且$b$为任意实数;③$a$为任意实数且$b+1=1$,解得$b=0$且$a$为任意实数;④$a$为任意实数且$b+1=0$,解得$b=-1$且$a$为任意实数。