《2025年绩优学案九年级数学上册人教版》

【例1】 如图21-3-3-1,要对一块长60m、宽40m的矩形荒地ABCD进行绿化和硬化。设计方案中,矩形P,Q为两块绿地,其余为硬化路面,P,Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形ABCD面积的$\frac{1}{4}$,求P,Q两块绿地周围的硬化路面的宽。

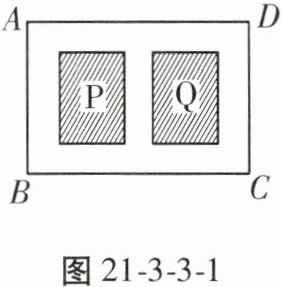
解题关键 利用“两块绿地面积和 = $\frac{1}{4}S_{矩形ABCD}$”列出方程求解。

答案： 解:设P,Q两块绿地周围的硬化路面的宽都为x m,根据题意,得(60 - 3x)×(40 - 2x)=60×40×$\frac{1}{4}$,解得$x_1=10$,$x_2=30$。经检验,$x_2=30$不符合题意,舍去。所以两块绿地周围的硬化路面的宽都为10 m。

【例2】 如图21-3-3-2,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪。要使草坪的面积为$540m^2,$求道路的宽。

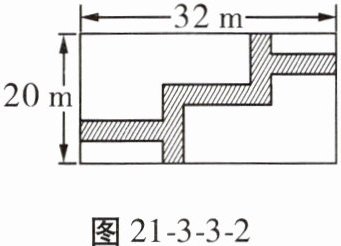
解题关键 数形结合,平移转化。

答案：
解:利用平移,原图可转化为下图,设道路的宽为x m,根据题意得(20 - x)(32 - x)=540,整理得$x^2 - 52x + 100=0$,解得$x_1=50$(舍去),$x_2=2$。即道路的宽为2 m。