《2025年绩优学案九年级数学上册人教版》

7. 某校举办“书香相伴,香满校园”的读书活动。其中9月份借阅图书550本,11月份借阅图书792本,如果每月借阅图书数量的增长率相同,设每月借阅图书数量的增长率为$x$,则$x$的值为(A)
A.20%
B.30%
C.40%
D.50%

答案： A

8. 某汽车销售公司6月份销售某厂家的汽车,在一定范围内,每部汽车的进价与销售量有如下关系：若当月仅售出1部汽车,则该部汽车的进价为27万元,每多售出1部,所有售出的汽车的进价均降低0.1万元,月底厂家根据销售量一次性返利给销售公司,销售量在10部以内(含10部),每部返利0.5万元；销售量在10部以上,每部返利1万元。
(1)若该公司当月售出3部汽车,则每部汽车的进价为26.8万元；
(2)如果汽车的售价为28万元/部,该公司计划当月盈利12万元,那么需要售出多少部汽车？(盈利$=销售利润+$返利)
设需要售出x部汽车,由题意可知,每部汽车的销售利润为$28-[27 - 0.1(x - 1)]=(0.1x + 0.9)$(万元)。当$0 ＜ x\leqslant10$时,根据题意,得$x(0.1x + 0.9)+0.5x = 12$,整理得$x^2 + 14x - 120 = 0$,解得$x_1=-20$(不合题意,舍去),$x_2 = 6$;当$x ＞ 10$时,根据题意,得$x(0.1x + 0.9)+x = 12$,整理得$x^2 + 19x - 120 = 0$,解得$x_1=-24$(不合题意,舍去),$x_2 = 5$,因为$5 ＜ 10$,所以$x_2 = 5$舍去,则需要售出6部汽车。

答案：
(1)26.8
(2)设需要售出x部汽车,由题意可知,每部汽车的销售利润为$28-[27 - 0.1(x - 1)]=(0.1x + 0.9)$(万元)。当$0 ＜ x\leqslant10$时,根据题意,得$x(0.1x + 0.9)+0.5x = 12$,整理得$x^2 + 14x - 120 = 0$,解得$x_1=-20$(不合题意,舍去),$x_2 = 6$;当$x ＞ 10$时,根据题意,得$x(0.1x + 0.9)+x = 12$,整理得$x^2 + 19x - 120 = 0$,解得$x_1=-24$(不合题意,舍去),$x_2 = 5$,因为$5 ＜ 10$,所以$x_2 = 5$舍去,则需要售出6部汽车。

9. 某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同。
(1)求该种商品每次降价的百分率；
(2)若该种商品的进价为300元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3210元,第一次降价后至少要售出该种商品多少件？

答案：
(1)设该种商品每次降价的百分率为x,依题意得$400×(1 - x)^2 = 324$,解得$x = 0.1$或$x = 1.9$(舍去)。答:该种商品每次降价的百分率为10%。
(2)设第一次降价后售出该种商品m件,则第二次降价后售出该种商品$(100 - m)$件。第一次降价后的单件利润为$400×(1 - 10\%)-300 = 60$(元);第二次降价后的单件利润为$324 - 300 = 24$(元)。依题意得$60m + 24×(100 - m)=36m + 2400\geqslant3210$,解得$m\geqslant22.5$,
∴$m\geqslant23$。答:为使两次降价销售的总利润不少于3210元,第一次降价后至少要售出该种商品23件。

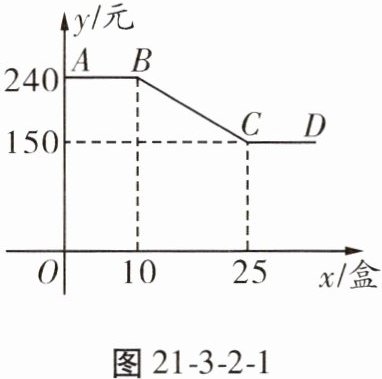
10. 中秋节前夕,某公司的李会计受公司委派去超市购买若干盒月饼,超市给出了某种月饼不同购买数量的价格优惠,如图21-3-2-1,折线$ABCD表示购买这种月饼每盒的价格y$(元)与盒数$x$(盒)之间的函数关系。
(1)当购买这种月饼不超过10盒时,一盒月饼的价格为240元；
(2)求出当$10 ＜ x ＜ 25$时,$y与x$之间的函数关系式；
(3)当时李会计支付了3600元购买这种月饼,那么李会计买了多少盒这种月饼？

(2)当$10 ＜ x ＜ 25$时,设$y = kx + b$,将B(10,240),C(25,150)代入$y = kx + b$,得$\begin{cases}10k + b = 240\\25k + b = 150\end{cases}$解得$\begin{cases}k=-6\\b = 300\end{cases}$
∴当$10 ＜ x ＜ 25$时,$y=-6x + 300$。
(3)
∵$3600÷240 = 15$(盒),$3600÷150 = 24$(盒),
∴收费标准在BC段。根据题意得$(-6x + 300)x = 3600$,解得$x_1 = 20$,$x_2 = 30$(舍去)。答:李会计买了20盒这种月饼。

答案：
(1)240
(2)当$10 ＜ x ＜ 25$时,设$y = kx + b$,将B(10,240),C(25,150)代入$y = kx + b$,得$\begin{cases}10k + b = 240\\25k + b = 150\end{cases}$解得$\begin{cases}k=-6\\b = 300\end{cases}$
∴当$10 ＜ x ＜ 25$时,$y=-6x + 300$。
(3)
∵$3600÷240 = 15$(盒),$3600÷150 = 24$(盒),
∴收费标准在BC段。根据题意得$(-6x + 300)x = 3600$,解得$x_1 = 20$,$x_2 = 30$(舍去)。答:李会计买了20盒这种月饼。