第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
$\left\{\begin{array}{l}(\quad)个小杯的容量+(\quad)个大杯的容量=720毫升 \\小杯的容量×3=大杯的容量 \end{array}\right.$
\end{array}\right.$
可以假设把720毫升果汁全部倒入小杯,把1个大杯看作3个小杯,一共倒了( )小杯。
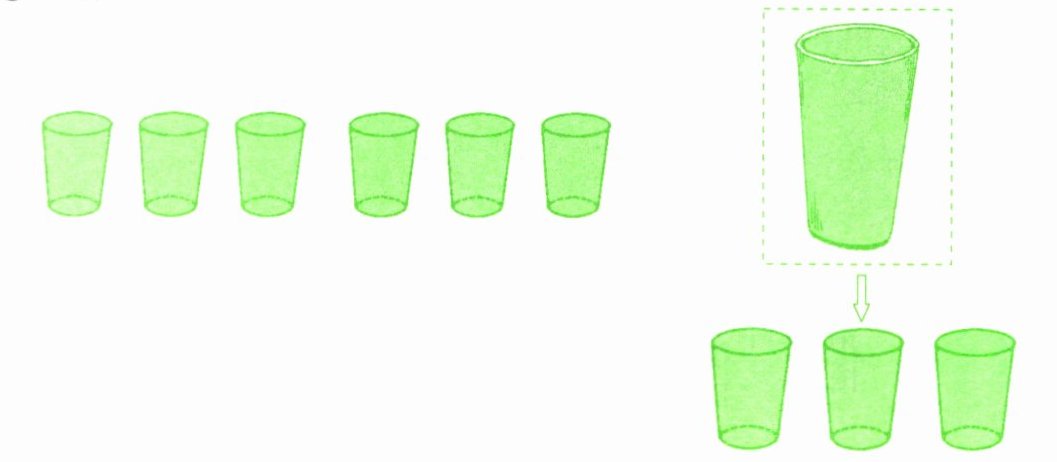
小杯容量:$720÷(6 + 3) =\_\_\_\_$(毫升)

大杯容量:$\_\_\_\_÷\dfrac{1}{3} =\_\_\_\_$(毫升)


借助线段图分析或列方程也可以解决这个问题,请你试试看吧。
回顾解题的过程,你有什么体会?在以前的学习中,我们曾经运用假设的策略解决过哪些问题?想一想,和同学交流一下你的想法吧!
 \end{array}\right.$
\end{array}\right.$可以假设把720毫升果汁全部倒入小杯,把1个大杯看作3个小杯,一共倒了( )小杯。

小杯容量:$720÷(6 + 3) =\_\_\_\_$(毫升)

大杯容量:$\_\_\_\_÷\dfrac{1}{3} =\_\_\_\_$(毫升)


借助线段图分析或列方程也可以解决这个问题,请你试试看吧。
回顾解题的过程,你有什么体会?在以前的学习中,我们曾经运用假设的策略解决过哪些问题?想一想,和同学交流一下你的想法吧!
答案:
6;1;9;80;80;240
列方程解法:
解:设小杯容量为$x$毫升,则大杯容量为$3x$毫升。
$6x + 3x = 720$
$9x = 720$
$x = 80$
大杯容量:$3×80 = 240$(毫升)
体会:运用假设策略可将不同量转化为相同量,使问题简化。
举例:鸡兔同笼问题、图形转化问题。
列方程解法:
解:设小杯容量为$x$毫升,则大杯容量为$3x$毫升。
$6x + 3x = 720$
$9x = 720$
$x = 80$
大杯容量:$3×80 = 240$(毫升)
体会:运用假设策略可将不同量转化为相同量,使问题简化。
举例:鸡兔同笼问题、图形转化问题。
1. 学校体育室买来5个篮球和8个排球,已知篮球的单价是排球单价的2倍。
(1) 1个篮球可以换成( )个排球,5个篮球可以换成( )个排球,体育室相当于一共买了( )个排球。
(2) 8个排球可以换成( )个篮球,体育室相当于一共买了( )个篮球。
(1) 1个篮球可以换成( )个排球,5个篮球可以换成( )个排球,体育室相当于一共买了( )个排球。
(2) 8个排球可以换成( )个篮球,体育室相当于一共买了( )个篮球。
答案:
1.
(1)2 10 18
(2)4 9
(1)2 10 18
(2)4 9
查看更多完整答案,请扫码查看


