《2025年单元评价卷宁波出版社五年级数学上册人教版》

1. 一条水渠横截面是梯形,渠深 0.7 米,渠底宽 1.3 米,渠口宽 2 米,它的横截面积是多少平方米？

答案： 答题卡：
根据梯形面积公式：$S=(a+b)h÷2$（其中$a$为上底，$b$为下底，$h$为高），已知水渠横截面是梯形，渠深$0.7$米即高$h = 0.7$米，渠底宽$1.3$米即下底$b = 1.3$米，渠口宽$2$米即上底$a = 2$米。
将数值代入公式可得：
$S=(2 + 1.3)×0.7÷2$
$=3.3×0.7÷2$
$=2.31÷2$
$= 1.155$（平方米）
答：它的横截面积是$1.155$平方米。

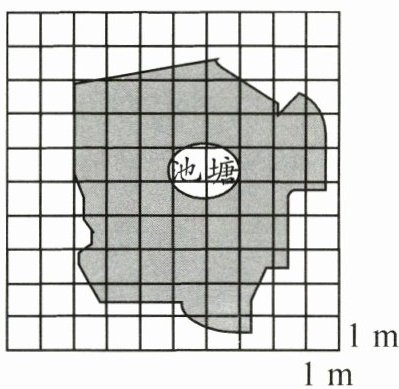
2. 如图,池塘的面积大约是多少平方米？

答案： 可通过数方格的方法估算池塘面积，满格有 22 格，不满格有 18 格，不满格按半格计算，则池塘面积大约为：$22×1 + 18×0.5 = 22 + 9 = 31$（平方米）。
故池塘的面积大约是 31 平方米。

3. 如图,四边形 ABCD 是一个直角梯形,它的面积公式为$ S= \frac{1}{2}(AB+CD)BC $。
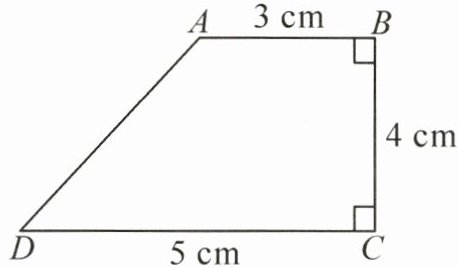
(1)如果四边形 ABCD 的边随着顶点的移动而变化,那么当点 B 移动到点 A 时,点 A,B 重合,这时图形变为(三角形),面积是(10cm²)。
(2)点 B 向右平移一段距离,四边形 ABCD 可以变为平行四边形。如果四边形 ABCD 要变为长方形,可以怎么移动？请在图中作出草图,并计算长方形的面积。

将点B向右平移2cm，使AB=CD=5cm。此时四边形ABCD为长方形，面积=5×4=20cm²。

答案：
(1)三角形；10cm²
(2)将点B向右平移2cm，使AB=CD=5cm。此时四边形ABCD为长方形，面积=5×4=20cm²。