2. 请测量并用不同方法计算同一个梯形的面积。

(1)按梯形公式计算 (2)分成两个三角形计算 (3)分成一个三角形和一个平行四边形计算

(1)按梯形公式计算 (2)分成两个三角形计算 (3)分成一个三角形和一个平行四边形计算
答案:
假设测量梯形的上底为3厘米,下底为5厘米,高为4厘米(具体数值根据实际测量可能不同,以下为示例)。
(1)按梯形公式计算
$S=(a+b)h÷2$
$=(3 + 5)×4÷2$
$=8×4÷2$
$=16$(平方厘米)
(2)分成两个三角形计算
$S_1 = 3×4÷2÷2(假设按对角线分,其中一个以上底为底的三角形面积,这里假设等高分割,实际按测量) = 6÷2(若按此简单假设)= 3$(平方厘米,此为示例计算方式,实际应准确测量分割后底和高)
$S_2=5×4÷2÷2(同理由)=10÷2 = 5$(平方厘米,同上)
准确计算:设分割后两三角形高都为梯形高4厘米,底分别为3厘米和5厘米,$S = 3×4÷2+5×4÷2=6 + 10=16$(平方厘米)
(3)分成一个三角形和一个平行四边形计算
假设平行四边形底为3厘米,高为4厘米,三角形底为$5 - 3 = 2$厘米,高为4厘米。
平行四边形面积$S_1 = 3×4 = 12$(平方厘米)
三角形面积$S_2=(5 - 3)×4÷2=4$(平方厘米)
梯形面积$S = S_1+S_2=12 + 4 = 16$(平方厘米)
综上,三种方法计算梯形面积均为16平方厘米。
(1)按梯形公式计算
$S=(a+b)h÷2$
$=(3 + 5)×4÷2$
$=8×4÷2$
$=16$(平方厘米)
(2)分成两个三角形计算
$S_1 = 3×4÷2÷2(假设按对角线分,其中一个以上底为底的三角形面积,这里假设等高分割,实际按测量) = 6÷2(若按此简单假设)= 3$(平方厘米,此为示例计算方式,实际应准确测量分割后底和高)
$S_2=5×4÷2÷2(同理由)=10÷2 = 5$(平方厘米,同上)
准确计算:设分割后两三角形高都为梯形高4厘米,底分别为3厘米和5厘米,$S = 3×4÷2+5×4÷2=6 + 10=16$(平方厘米)
(3)分成一个三角形和一个平行四边形计算
假设平行四边形底为3厘米,高为4厘米,三角形底为$5 - 3 = 2$厘米,高为4厘米。
平行四边形面积$S_1 = 3×4 = 12$(平方厘米)
三角形面积$S_2=(5 - 3)×4÷2=4$(平方厘米)
梯形面积$S = S_1+S_2=12 + 4 = 16$(平方厘米)
综上,三种方法计算梯形面积均为16平方厘米。
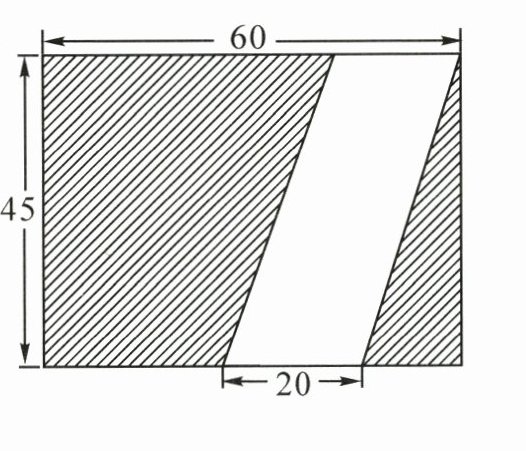
3. 求下面图形中阴影部分的面积。(单位:厘米)
(1)
(2)求下面图形的面积。(单位:厘米)(至少用两种方法)
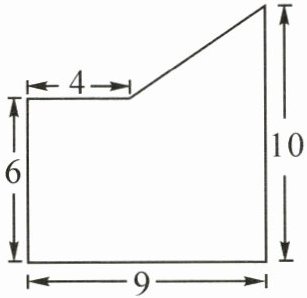
(1)

(2)求下面图形的面积。(单位:厘米)(至少用两种方法)

答案:
3.
(1)
60×45 - 20×45
= (60-20)×45
= 40×45
= 1800(平方厘米)
(2)
方法一:
9×6 + (9-4)×(10-6)÷2
= 54 + 5×4÷2
= 54 + 10
= 64(平方厘米)
方法二:
4×6 + (6+10)×(9-4)÷2
= 24 + 16×5÷2
= 24 + 40
= 64(平方厘米)
(1)
60×45 - 20×45
= (60-20)×45
= 40×45
= 1800(平方厘米)
(2)
方法一:
9×6 + (9-4)×(10-6)÷2
= 54 + 5×4÷2
= 54 + 10
= 64(平方厘米)
方法二:
4×6 + (6+10)×(9-4)÷2
= 24 + 16×5÷2
= 24 + 40
= 64(平方厘米)
查看更多完整答案,请扫码查看


