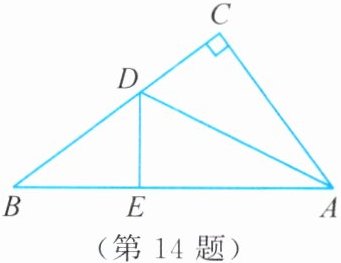
14. 如图,直角三角形纸片的两直角边$AC = 6cm$,$BC = 8cm$。现将直角边$AC沿AD$折叠,使它落在斜边$AB$上,点$C与点E$重合。求$CD$的长。
]
]

答案:
由已知得AB=10cm,∠AED=∠C=Rt∠,AE=AC=6cm,DE=DC,则BE=4cm。在Rt△BED中,$BE^{2}+DE^{2}=BD^{2}$,即$4^{2}+CD^{2}=(8 - CD)^{2}$,解得CD=3cm。
15. 已知:如图,$AC$,$BD交于点O$,$\angle A= \angle D = 90^{\circ}$,$AC = BD$。求证:$OB = OC$。
]

]

答案:
连结BC。可证Rt△ABC≌Rt△DCB,所以∠ACB=∠DBC,从而OB=OC。
16. 已知:如图,在$\triangle ABC$中,$BF\perp AC于点F$,$CG\perp AB于点G$,$D是BC$的中点,$DE\perp FG于点E$。求证:$GE = EF$。
]

]

答案:
连结DG,DF。由CG⊥AB,D是BC的中点,得$DG=\frac{1}{2}BC$。同理,$DF=\frac{1}{2}BC$。所以DG=DF。而DE⊥FG,所以GE=EF。
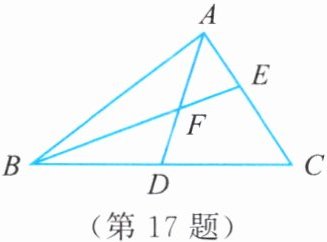
17. 已知:如图,在$\triangle ABC$中,$AD是BC$边上的中线,$F是AD$上一点,延长$BF$,交$AC于点E$,且$AE = EF$。求证:$BF = AC$。
]
]

答案:
如图,延长FD到G,使DG=DF,连结CG。因为AD是BC边的中线,所以BD=CD。又因为∠FDB=∠GDC,所以△BDF≌△CDG(SAS),所以BF=CG,∠BFD=∠G。因为AE=EF,所以∠EAF=∠EFA=∠BFD,所以∠G=∠CAG,所以AC=CG,所以BF=AC。
如图,延长FD到G,使DG=DF,连结CG。因为AD是BC边的中线,所以BD=CD。又因为∠FDB=∠GDC,所以△BDF≌△CDG(SAS),所以BF=CG,∠BFD=∠G。因为AE=EF,所以∠EAF=∠EFA=∠BFD,所以∠G=∠CAG,所以AC=CG,所以BF=AC。

查看更多完整答案,请扫码查看


