《2025年作业本浙江教育出版社八年级数学上册浙教版》

9. 如图,在$\triangle ABC$中,$\angle C = 29^{\circ}$,$D为AC$上一点,且$AB = AD$,$DB = DC$。求$\angle A$的度数。
]

答案： 因为BD=DC,∠C=29°,所以∠DBC=∠C=29°,所以∠ADB=2∠C=58°。又因为AD=DB,所以∠A=180° - 2∠ADB=64°。

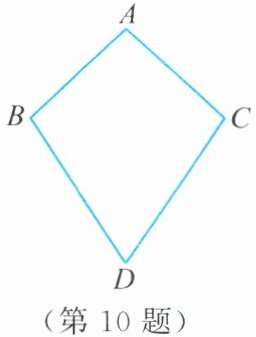
10. 如图,已知$AB = AC$,$\angle B= \angle C$,则$BD = CD$。请说明理由。
]

答案： 连结BC。由AB=AC,得∠ABC=∠ACB。又因为∠ABD=∠ACD,所以∠DBC=∠DCB。所以BD=CD。

11. 一个等腰三角形的底边长为5,一条腰上的中线把其周长分成的两部分的差为3,则这个等腰三角形的腰长为(B)。
A.$2$
B.$8$
C.$2或8$
D.$10$

答案： B

12. 已知两条线段的长为$3cm和4cm$,当第三条线段的长为5或$\sqrt{7}$ $cm$时,这三条线段就能组成一个直角三角形。

答案： 5或$\sqrt{7}$

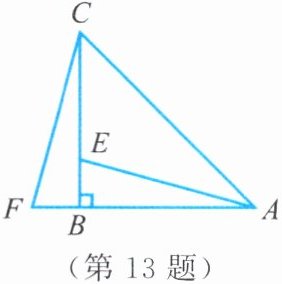
13. 如图,在$\triangle ABC$中,$AB = CB$,$\angle ABC = 90^{\circ}$。$F为AB$延长线上一点,点$E在BC$上,且$BE = BF$。
(1) 求证：$\triangle ABE\cong\triangle CBF$。
(2) 若$\angle CAE = 30^{\circ}$,求$\angle ACF$的度数。
]

答案： （1）由BE=BF,∠CBF=∠ABE=90°,AB=CB,得△ABE≌△CBF(SAS)。（2）由AB=BC,∠ABC=90°,得∠CAB=∠ACB=45°,所以∠BAE=∠CAB - ∠CAE=15°,所以∠BCF=∠BAE=15°,所以∠ACF=∠BCF+∠ACB=15°+45°=60°。