《2025年作业本浙江教育出版社八年级数学上册浙教版》

6. 在$\triangle ABC$中,$AB = c$,$AC = b$,$BC = a$。有下列条件：
①$a^{2}= b^{2}+c^{2}$；②$\angle A= \angle B-\angle C$；③$\angle A:\angle B:\angle C = 3:4:5$；
④$a:b:c = 3:4:5$；⑤$\angle A= \frac{1}{2}\angle B= \frac{2}{3}\angle C$。
其中可以判定$\triangle ABC$为直角三角形的有①②④(填序号)。

答案： ①②④

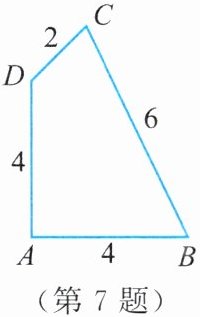
7. 如图,在四边形$ABCD$中,$\angle A = 90^{\circ}$,$AD = AB = 4$,$BC = 6$,$CD = 2$。求$\angle ADC$的度数。

答案： 连结BD。由$\angle A=90^{\circ},AD=AB=4$，可得$BD=4\sqrt{2},\angle ADB=45^{\circ}$。又因为$CD=2,BC=6$，所以$CD^{2}+BD^{2}=CB^{2}$，所以$\angle CDB=90^{\circ}$。所以$\angle ADC=\angle ADB+\angle CDB=135^{\circ}$。

8. 已知如下数表：

(1) 观察$a$,$b$,$c与n$之间的关系,用含自然数$n(n ＞ 1)$的代数式表示：
$a= $$n^{2}-1$,$b= $$2n$,$c= $$n^{2}+1$。
(2) 试猜想：以$a$,$b$,$c$为边的三角形是直角三角形吗？请说明理由。
以a,b,c为边的三角形是直角三角形。理由如下：因为$a^{2}+b^{2}=(n^{2}-1)^{2}+(2n)^{2}=n^{4}+2n^{2}+1$，$c^{2}=(n^{2}+1)^{2}=n^{4}+2n^{2}+1$，所以$a^{2}+b^{2}=c^{2}$。所以以a,b,c为边的三角形是直角三角形。

答案： （1）$n^{2}-1;2n;n^{2}+1$（2）以a,b,c为边的三角形是直角三角形。理由如下：因为$a^{2}+b^{2}=(n^{2}-1)^{2}+(2n)^{2}=n^{4}+2n^{2}+1$，$c^{2}=(n^{2}+1)^{2}=n^{4}+2n^{2}+1$，所以$a^{2}+b^{2}=c^{2}$。所以以a,b,c为边的三角形是直角三角形。