《2025年作业本浙江教育出版社八年级数学上册浙教版》

6. (多选题)在$\triangle ABC$中,$P为边BC$上一点,且$PB = PC$。下列条件能使$\triangle ABC$为直角三角形的是(AB)。
A.$∠BAP = ∠ABP$
B.$AP = PC$
C.$∠PAC = ∠B$
D.$AP⊥BC$

答案： AB

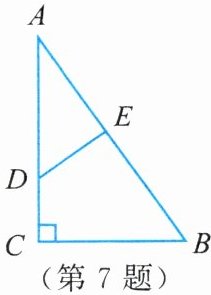
7. 如图,在$\triangle ABC$中,$∠C = 90^{\circ}$,点$D$,$E分别在边AC$,$AB$上。若$∠B = ∠ADE$,有下列说法：
①$∠AED = 90^{\circ}$；②$∠A与∠ADE$互为余角；
③$BC = BE$；④$∠CDE与∠B$互为补角。
其中说法正确的有①②④。

答案： ①②④

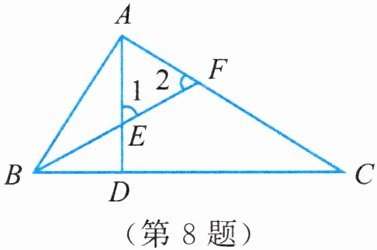
8. 已知：如图,$AD$,$BF分别是\triangle ABC$的高线与角平分线,$BF与AD交于点E$,$∠1 = ∠2$。求证：$\triangle ABC$是直角三角形。

答案： 因为∠1=∠2,∠1=∠BED,所以∠2=∠BED。因为BF平分∠ABC,所以∠ABF=∠CBF。因为AD⊥BC,所以∠CBF+∠BED=90°。所以∠ABF+∠2=90°,即△ABC为直角三角形。

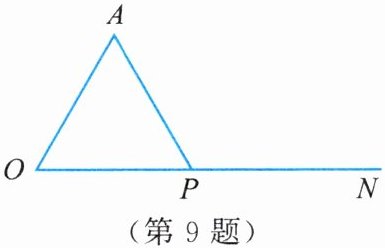
9. 如图,已知$∠AON = 60^{\circ}$,$AO = 10$,$P是射线ON$上一动点。
(1)当$OP = $5或20时,$\triangle AOP$为直角三角形。
(2)设$OP = x$,则$x$满足0＜x＜5或x＞20时,$\triangle AOP$为钝角三角形。

答案：
(1)5或20
(2)0＜x＜5或x＞20