《2025年作业本浙江教育出版社八年级数学上册浙教版》

1. 在$\triangle ABC$中,已知$∠A = ∠B + ∠C$,则$∠A$的度数为90°,$\triangle ABC$是直角三角形。

答案： 90°;直角

2. 在$\triangle ABC$中,若$∠A = \frac{1}{2}∠B = \frac{1}{3}∠C$,则$\triangle ABC$是(B)。
A.等腰三角形
B.直角三角形
C.锐角三角形
D.钝角三角形

答案： B

3. 如果一个三角形的一个顶点是它的三条高线的交点,那么这个三角形是(B)。
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等边三角形

答案： B

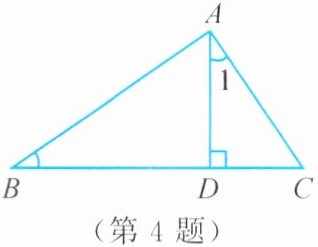
4. 已知：如图,在$\triangle ABC$中,$AD⊥BC于点D$,$∠1 = ∠B$。求证：$\triangle ABC$为直角三角形。

答案： 因为AD⊥BC,所以∠1+∠C=90°。又因为∠1=∠B,所以∠B+∠C=90°,所以△ABC为直角三角形。

5. 已知命题：“若一个三角形三个内角的度数之比为$3:4:5$,则这个三角形是直角三角形。”判断这个命题的真假,并说明理由。

答案： 假命题。理由如下:设△ABC的三个内角为∠A,∠B,∠C,且∠A:∠B:∠C =3:4:5,得∠C=75°,所以△ABC为锐角三角形。