《2025年作业本浙江教育出版社八年级数学上册浙教版》

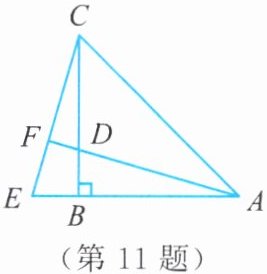
11. 如图,在$\triangle ABC$中,$\angle ABC = 90^{\circ}$,$AB = BC$,$D是BC$上的一点,$E是AB$延长线上的一点,且$BD = BE$,$AD的延长线交CE于点F$。$AF与CE$垂直吗？为什么？

答案： AF⊥CE。理由如下：由∠ABC=90°，可得∠CBE=90°，所以∠ABC=∠CBE。又知BD=BE，AB=BC，可得△ABD≌△CBE(SAS)，所以∠BCE=∠BAD。因为∠ABC+∠BAD+∠BDA=180°，∠DFC+∠BCE+∠CDF=180°，又因为∠BDA=∠CDF，所以∠DFC=∠ABC=90°，即AF⊥CE。

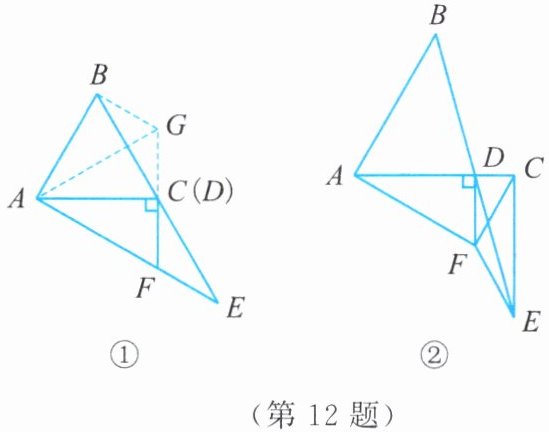
12. 已知$\angle BAC = \alpha(0^{\circ} \lt \alpha\leqslant 90^{\circ})$,$AB = AC$,$D是线段AC$上的动点。延长$BD至点E$,使得$BD = DE$,连结$CE$。过点$D作DF\perp AC$,交$CE的垂直平分线于点F$,连结$AF$,$CF$,$EF$。探究$\angle DAF与\angle BAC$的数量关系。
(1)如图①,当点$D与点C$重合时,小明作如下探究：延长$FD至点G$,使得$DG = DF$,连结$BG$,$AG$。发现一些全等三角形,如$\triangle BGD\cong\triangle EFD$,$\triangle ABG\cong\triangle ADF$等,则$\angle DAF与\angle BAC$的数量关系为______。
(2)如图②,当点$D与点C$不重合时,猜想$\angle DAF与\angle BAC$的数量关系,并说明理由。

答案：
（1）∠DAF=$\frac{1}{2}$∠BAC（2）猜想：∠DAF=$\frac{1}{2}$∠BAC。理由如下：如图，当点D在线段AC上时，延长FD到点G，使DG=DF，连结BG，AG。由DF⊥AC，得∠ADF=∠ADG=90°。在△ADF和△ADG中，由DG=DF，∠ADF=∠ADG=90°，AD=AD，得△ADF≌△ADG(SAS)，所以∠DAF=∠DAG，AF=AG。在△BGD和△EFD中，DG=DF，∠BDG=∠EDF，BD=DE，所以△BGD≌△EFD(SAS)，所以BG=EF。因为点F在CE的垂直平分线上，所以EF=CF，所以BG=CF。在△ABG和△ACF中，由AB=AC，AG=AF，BG=CF，证得△ABG≌△ACF(SSS)，所以∠BAG=∠DAF，所以∠BAC=∠BAG+∠DAG=2∠DAF，所以∠DAF=$\frac{1}{2}$∠BAC。