《2025年作业本浙江教育出版社八年级数学上册浙教版》

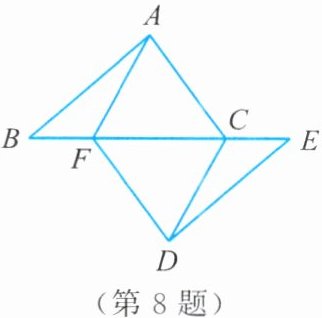
8. 已知：如图,点$B$,$F$,$C$,$E$在一条直线上,$FB = CE$,$AB = DE$,$AC = DF$。
求证：
(1)$\triangle ABC\cong\triangle DEF$；
(2)$AF = CD$。

答案： （1）由FB=CE，可得BC=EF。又因为AB=DE，AC=DF，所以△ABC≌△DEF。（2）由（1）得∠B=∠E。又由AB=DE，FB=CE，可证△ABF≌△DEC(SAS)，所以AF=CD。

9. 如图,$AD是\triangle ABC中\angle BAC$的平分线,$DE\perp AB于点E$,$DF\perp AC于点F$。若$S_{\triangle ABC} = 7$,$DE = 2$,$AB = 4$,则$AC$的长是3。

答案： 3

10. 如图。
命题一：如果$AD既是BC$边上的高线,又是$\angle BAC$的平分线,那么$\triangle ABD\cong\triangle ACD$。
命题二：如果$AD既是BC$边上的高线,又是$BC$边上的中线,那么$\triangle ABD\cong\triangle ACD$。
(1)证明上述两个命题。
(2)想一想,分别满足上述两个命题的条件,你还能推得哪些共同的结论？

答案： （1）命题一的证明：由已知，可得∠ADB=∠ADC，∠BAD=∠CAD。从而可证△ABD≌△ACD（ASA）。命题二的证明：由已知，可得∠ADB=∠ADC，BD=CD。从而可证△ABD≌△ACD(SAS)。（2）共同的结论有：AB=AC，∠B=∠C(答案不唯一)。