《2025年作业本浙江教育出版社八年级数学上册浙教版》

6.如图,已知![△ABC ],![P ]为边![AB ]上一点。请用直尺和圆规在边![AC ]上作一点![E ],使![AE + EP = AC ]。(保留作图痕迹,不写作法)

答案：
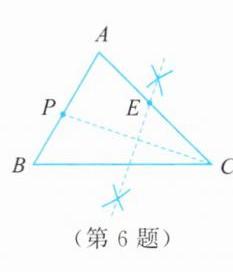
如图，连结PC,作线段PC的垂直平分线，交AC于点E,E 为所求作的点。

7. (多选题)若直线![PE ]是线段![AB ]的垂直平分线,则下列说法一定正确的是(ABC)。
A.![EA = EB ,PA = PB ]
B.![∠PAE = ∠PBE ]
C.![∠APE = ∠BPE ]
D.![∠APB = ∠AEB ]

答案： ABC

8.如图,在![△ABC ]中,边![AC ]的垂直平分线分别交![AB ,AC ]于点![M ,N ]。已知![△ABC ]与![△BCM ]的周长分别为22 cm和14 cm,求![CN ]的长。

答案： 由题意得MA=MC,AN=CN。因为△ABC的周长=AC +BC+AB=22(cm),△BCM的周长=CM+BC+BM=MA+BM+BC=BC+AB=14(cm),所以AC=8(cm),所以CN=$\frac{1}{2}$AC=4(cm)。

9.如图,在![△ABC ]中,![AB = 6 ,AC = 5 ]。直线![m ]是![BC ]边的垂直平分线,![P ]是直线![m ]上的一动点,求![△ACP ]的周长的最小值。

答案： 连结BP。因为直线m是△ABC中BC边的垂直平分线，所以BP=CP,所以△ACP的周长=AP+PC+AC=BP+AP+AC≥AB+AC。所以当A,B,P 三点共线时,△ACP的周长最小,即△ACP的周长的最小值为AB+AC=11。