《2025年作业本浙江教育出版社八年级数学上册浙教版》

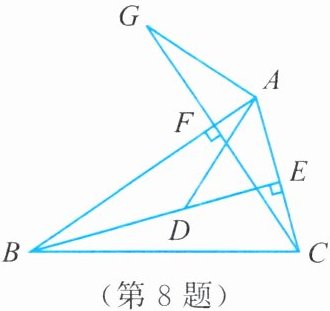
8. 如图,在△ABC 中,BE,CF 分别是 AC,AB 边上的高线。在 BE 上取一点 D,使得 BD = AC,在 CF 的延长线上取一点 G,使得 CG = AB,连结 AD,AG。
(1)求证：△AGC≌△DAB。
(2)判断线段 AD 和 AG 有何特殊的位置关系,并说明理由。

答案： （1）因为 BE,CF 分别是 AC,AB 边上的高线,所以∠BEA=90°,∠CFA=90°,所以∠ACG+∠CAB=90°,∠DBA+∠CAB=90°,所以∠ACG=∠DBA。又因为 AC=DB,CG=AB,所以△AGC≌△DAB(SAS)。
（2）AG⊥AD。理由如下:因为△AGC≌△DAB,所以∠G=∠BAD。又因为∠G+∠GAB=90°,所以∠BAD+∠GAB=90°,即∠GAD=90°,所以 AG⊥AD。

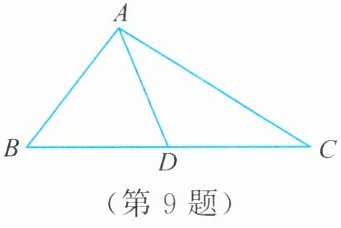
9. 如图,在△ABC 中,AB = 5,AC = 9,AD 是 BC 边上的中线,求 AD 的取值范围。

答案： 延长 AD 至点 E,使 DE=AD,连结 BE。可证△BDE≌△CDA,得到 BE=CA=9,则 9-5＜AE＜9+5,即 2＜AD＜7。