1. 如图,AD 与 BC 相交于点 O,AO = DO。若要判定△AOB≌△DOC,且只能添加一个条件,这个条件是

BO=CO,答案不唯一
。
答案:
BO=CO,答案不唯一
2. 如图,已知 BC 是△ABC 和△DBC 的公共边,若根据“SAS”来说明△ABC≌△DBC,则需要补充的条件是(

A.AB = DB,∠1 = ∠2
B.AB = DB,∠3 = ∠4
C.AB = DB,∠A = ∠D
D.∠1 = ∠2,∠3 = ∠4
B
)。
A.AB = DB,∠1 = ∠2
B.AB = DB,∠3 = ∠4
C.AB = DB,∠A = ∠D
D.∠1 = ∠2,∠3 = ∠4
答案:
B
3. 如图,已知 C 是 AB 的中点,∠A = ∠B,AD = BE,则∠D = ∠E。请完成下面的说理过程(填空)。
解:因为 C 是 AB 的中点,所以
在△ADC 和△BEC 中,
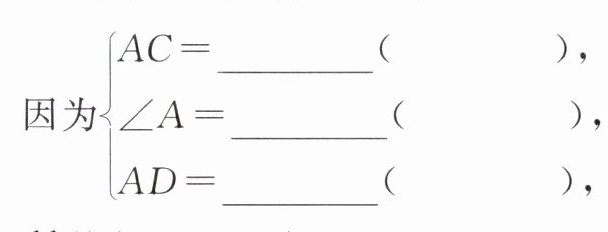
所以△ADC≌△BEC(
所以∠D = ∠E(

解:因为 C 是 AB 的中点,所以
AC
= BC
。在△ADC 和△BEC 中,

所以△ADC≌△BEC(
SAS
)。所以∠D = ∠E(
全等三角形的对应角相等
)。
答案:
AC=BC;BC(已证);∠B(已知);BE(已知);SAS;全等三角形的对应角相等
4. 已知:如图,在△ABC 和△DAE 中,D 是 AC 上一点,AD = AB,DE//AB,DE = AC。求证:AE = BC。


答案:
由 DE//AB,可得∠ADE=∠BAC。在△ADE和△BAC中,由 AD=BA,∠ADE=∠BAC,DE=AC,得△ADE≌△BAC(SAS),所以 AE=BC。
查看更多完整答案,请扫码查看


