《2025年能力培养与测试八年级数学上册人教版》

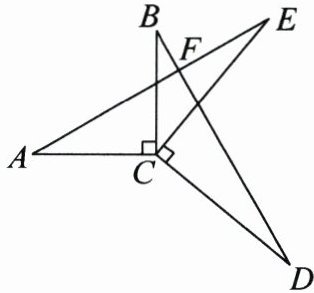
16. 如图， $ AC \perp BC $， $ DC \perp EC $， $ AC = BC $， $ DC = EC $， $ AE $ 与 $ BD $ 相交于点 $ F $.
（1）求证 $ AE = BD $；
（2）求 $ \angle AFD $ 的度数.

答案： （1）证明：
∵AC⊥BC，DC⊥EC，
∴∠ACB=∠ECD=90°.
∴∠ACB+∠BCE=∠BCE+∠ECD，即
∠ACE=∠BCD.
在△ACE和△BCD中，
$\begin{cases} AC = BC, \\ ∠ACE = ∠BCD, \\ EC = DC, \end{cases}$
∴△ACE≌△BCD (SAS).
∴AE=BD.
（2）解：设 AE 与 BC 相交于点 G (图略).
∵△ACE≌△BCD，
∴∠A=∠B.
又∠AGC=∠BGF，
∴∠BFA=∠ACB=90°.
∴∠AFD=90°.

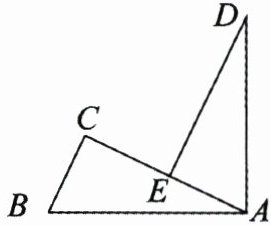
17. 如图， $ A $， $ E $， $ C $ 三点在同一条直线上，且 $ \triangle ABC \cong \triangle DAE $， $ AB $ 和 $ DA $ 是对应边， $ \angle B $ 和 $ \angle EAD $ 是对应角.
（1）线段 $ DE $， $ CE $， $ BC $ 有怎样的数量关系？请说明理由.
（2）当 $ \triangle ADE $ 满足什么条件时， $ DE // BC $？证明你的结论.

答案： （1）DE=CE+BC.
理由如下：
∵△ABC≌△DAE，
∴AE=BC，DE=AC.
∵A，E，C 三点在同一条直线上，
∴AC=AE+CE.
∴DE=CE+BC.
（2）当△ADE 满足∠AED=90°时，
DE//BC.
证明：
∵△ABC≌△DAE，∠AED=90°，
∴∠C=∠AED=90°，
∠DEC=180°-∠AED=90°.
∴∠C=∠DEC.
∴DE//BC.
故当△ADE 满足∠AED=90°时，
DE//BC.

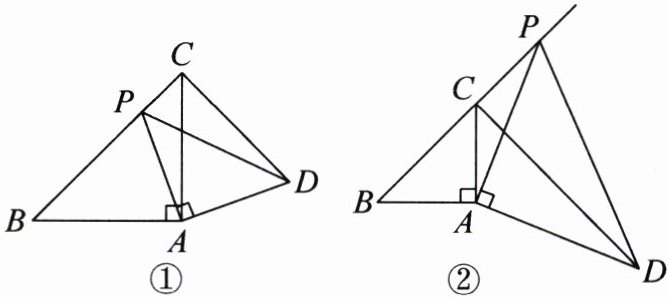
18. 如图，在等腰直角三角形 $ ABC $ 中， $ AB = AC $， $ \angle BAC = 90^{\circ} $， $ P $ 为射线 $ BC $ 上的一个动点（不与点 $ B $， $ C $ 重合），连接 $ AP $，以 $ AP $ 为直角边， $ A $ 为直角顶点，在 $ AP $ 右侧作等腰直角三角形 $ PAD $，连接 $ CD $.
（1）如图①，当点 $ P $ 在线段 $ BC $ 上时，求证 $ \triangle BAP \cong \triangle CAD $；
（2）如图②，当点 $ P $ 在线段 $ BC $ 的延长线上时，请直接写出线段 $ BP $ 和 $ CD $ 的数量关系与位置关系.

答案： （1）证明：
∵∠BAC=∠PAD=90°，
∴∠BAC-∠PAC=∠PAD-∠PAC，
即∠BAP=∠CAD.
在△BAP和△CAD中，
$\begin{cases} AB = AC, \\ ∠BAP = ∠CAD, \\ AP = AD, \end{cases}$
∴△BAP≌△CAD (SAS).
（2）BP=CD，BP⊥CD.