《2025年能力培养与测试八年级数学上册人教版》

19. 金师傅计划近期换车，他看中了两款价格相同的国产车.相关信息如下：

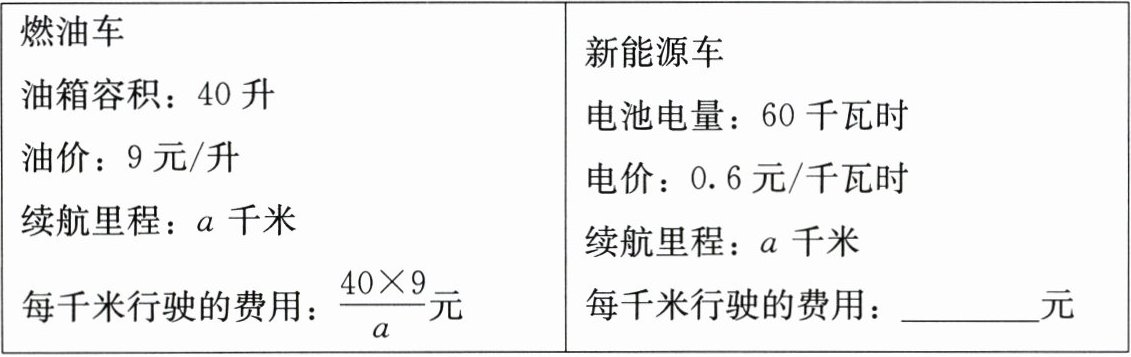
(1)用含$a$的代数式表示新能源车每千米行驶的费用；
(2)若燃油车每千米行驶的费用比新能源车多$0.54$元.
①分别求出这两款车每千米行驶的费用；
②若燃油车和新能源车每年的其他费用分别为$4800$元和$7500$元，则每年行驶里程为多少千米时，新能源车的年费用更低？(年费用$=$年行驶费用$+$年其他费用)

答案： 解：
(1)由题意，得
新能源车每千米行驶的费用为$\frac{60×0.6}{a}=$
$\frac{36}{a}$(元)，
即新能源车每千米行驶的费用为$\frac{36}{a}$元.
(2)①$\because$燃油车每千米行驶的费用比新能源
车多$0.54$元，
$\therefore\frac{40×9}{a}-\frac{36}{a}=0.54$.
方程两边乘$a$，得$360-36=0.54a$.
解得$a=600$.
检验：当$a=600$时，$a\neq0$.
$\therefore$原分式方程的解为$a=600$.
$\therefore\frac{40×9}{600}=0.6$，$\frac{36}{600}=0.06$.
答：燃油车每千米行驶的费用为$0.6$元，新能源车每千米行驶的费用为$0.06$元.
②设每年行驶里程为$x km$.
由题意，得$0.6x+4800＞0.06x+7500$.
解得$x＞5000$.
答：当每年行驶里程大于$5000 km$时，新能源车的年费用更低.

20. 定义：如果两个代数式的和与这两个代数式的积相等，那么称这两个代数式互为“关联式”.
(1)判断$\frac{2}{x + 1}$与$\frac{2}{x - 1}$是否互为“关联式”，并说明理由；
(2)求与$\frac{1}{2m + 1}(m\neq0)$互为“关联式”的代数式；
(3)填空：已知一个整式与一个最简分式互为“关联式”，请写出一组符合该条件的代数式可以是x与$\frac{x}{x-1}$.(只要写一组即可)

答案： 解：
(1)$\frac{2}{x+1}$与$\frac{2}{x-1}$不互为“关联式”.理
由如下：
$\because\frac{2}{x+1}+\frac{2}{x-1}=\frac{2x-2+2x+2}{(x+1)(x-1)}=$
$\frac{4x}{(x+1)(x-1)}$，
$\frac{2}{x+1}\cdot\frac{2}{x-1}=\frac{4}{(x+1)(x-1)}$，
而$\frac{4}{(x+1)(x-1)}\neq\frac{4x}{(x+1)(x-1)}$，
$\therefore\frac{2}{x+1}$与$\frac{2}{x-1}$不互为“关联式”.
(2)设$\frac{1}{2m+1}(m\neq0)$的关联式为$W$，
则$\frac{1}{2m+1}+W=\frac{W}{2m+1}$，
即$(\frac{1}{2m+1}-1)W=\frac{1}{2m+1}$，
$\frac{1-2m-1}{2m+1}W=\frac{1}{2m+1}$，
$\frac{-2m}{2m+1}W=\frac{1}{2m+1}$，
$\therefore-2mW=1$.
$\because m\neq0$，$\therefore W=-\frac{1}{2m}$.
(3)$x\frac{x}{x-1}$（答案不唯一）