《2025年能力培养与测试八年级数学上册人教版》

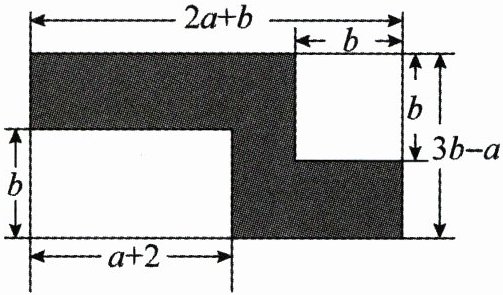
22. 如图，在长为$(2a + b)$m，宽为$(3b - a)$m的长方形铁片上，剪去一个长为$(a + 2)$m，宽为$b$m的小长方形铁片和一个边长为$b$m的正方形铁片.
（1）求剩余部分（即阴影部分）的面积；
（2）当$a = 6$，$b = 4$时，求图中阴影部分的面积.

答案： （1）由题意，得$S_{阴} = (2a + b)(3b - a) - b(a + 2) - b^2 = (2b^2 - 2a^2 + 4ab - 2b) m^2$.
（2）当$a = 6$，$b = 4$时，
$S_{阴} = 2b^2 - 2a^2 + 4ab - 2b$
$ = 2 × 4^2 - 2 × 6^2 + 4 × 6 × 4 - 2 × 4 = 48 (m^2)$.

23. 如图①，某学校准备装修三个不同的功能教室，购买了足够多的$A$（边长为$a$的小正方形），$B$（边长为$b$的大正方形），$C$（长为$b$，宽为$a$的长方形）三种类型的瓷砖来铺设教室$1$、教室$2$和教室$3$的地面.

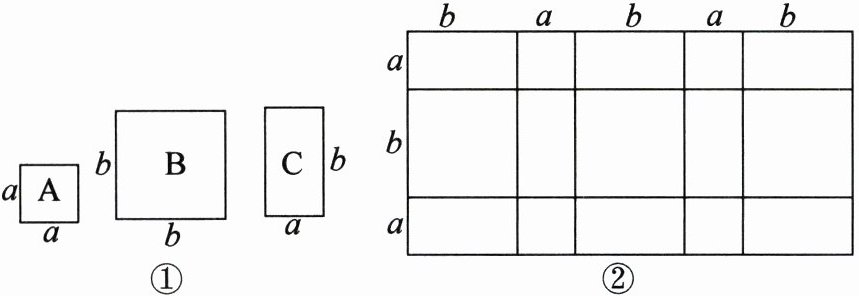
（1）教室$1$刚好按如图②的方式铺满，请求出教室$1$的面积$S$.（用含$a$，$b$的代数式表示）
（2）请通过计算说明：铺满长为$(3a + b)$，宽为$(a + 2b)$的教室$2$和长为$(4a + 2b)$，宽为$(2a + 3b)$的教室$3$共需要$A$，$B$，$C$三类瓷砖各多少块？（瓷砖均用整块，无空隙无重叠）.
（3）在（1）（2）的条件下，若一块$C$类瓷砖的周长为$16$，一块$B$类瓷砖和一块$A$类瓷砖的面积之差为$32$，求三个教室的面积之和.

答案： （1）由题意，得教室1的长为$(2a + 3b)$，宽为$(2a + b)$.
故教室1的面积$S = (2a + 3b)(2a + b)$
$ = 4a^2 + 2ab + 6ab + 3b^2$
$ = 4a^2 + 8ab + 3b^2$.
（2）由题意，得教室2和教室3的面积和为
$(3a + b)(a + 2b) + (4a + 2b)(2a + 3b)$
$ = 3a^2 + 6ab + ab + 2b^2 + 8a^2 + 12ab + 4ab + 6b^2$
$ = 11a^2 + 23ab + 8b^2$.
故共需要$A$类瓷砖11块，$B$类瓷砖8块，$C$类瓷砖23块.
（3）由题意可知$2a + 2b = 16$，$b^2 - a^2 = 32$.
所以$a + b = 8①$，$(b + a)(b - a) = 32$.
所以$b - a = 4②$.
$① + ②$，得$b = 6$.
把$b = 6$代入$①$，得$a = 2$.
所以三个教室的面积之和为
$4a^2 + 8ab + 3b^2 + 11a^2 + 23ab + 8b^2$
$ = 15a^2 + 11b^2 + 31ab$
$ = 15 × 2^2 + 11 × 6^2 + 31 × 2 × 6$
$ = 828$.