21. 如图,在$ \triangle ABC $中,$ \angle BAC = 90^{\circ} $,点$ D $在边$ AC $上,$ \angle ADB = 2\angle ABC $.
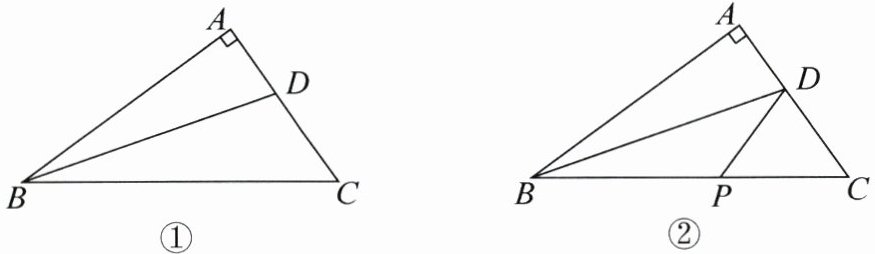
(1)请在图①中,画出$ \triangle ABC $关于$ AB $对称的$ \triangle ABE $;
(2)利用(1)中画出的图形,求证$ BD = CD + 2AD $;
(3)如图②,点$ P $在$ BC $边上,$ \angle ADB = \angle CDP $,将点$ P $和(1)画出的点$ E $相连,请直接写出$ \angle BPE $和$ \angle CPD $的关系式:

(1)请在图①中,画出$ \triangle ABC $关于$ AB $对称的$ \triangle ABE $;
(2)利用(1)中画出的图形,求证$ BD = CD + 2AD $;
(3)如图②,点$ P $在$ BC $边上,$ \angle ADB = \angle CDP $,将点$ P $和(1)画出的点$ E $相连,请直接写出$ \angle BPE $和$ \angle CPD $的关系式:
∠BPE + 2∠CPD = 180°
.
答案:
(1)解:△ABC关于AB对称的△ABE如图①所示.

(2) 证明:在AE上取点F,使AF = AD,连接BF,如图②所示.

∵∠DBC + ∠C = ∠ADB,
∠ADB = 2∠ABC = ∠EBC,
∠EBC = ∠EBD + ∠DBC,
∴∠DBC + ∠C = ∠DBC + ∠EBD.
∴∠C = ∠EBD.
∵∠C = ∠E,
∴∠EBD = ∠E.
∴BD = DE.
∵CA = AE,AD = AF,
∴CA - AD = AE - AF,即CD = EF.
∵DE = 2AD + EF,
∴BD = CD + 2AD.
(3) 解:∠BPE + 2∠CPD = 180°
(1)解:△ABC关于AB对称的△ABE如图①所示.

(2) 证明:在AE上取点F,使AF = AD,连接BF,如图②所示.

∵∠DBC + ∠C = ∠ADB,
∠ADB = 2∠ABC = ∠EBC,
∠EBC = ∠EBD + ∠DBC,
∴∠DBC + ∠C = ∠DBC + ∠EBD.
∴∠C = ∠EBD.
∵∠C = ∠E,
∴∠EBD = ∠E.
∴BD = DE.
∵CA = AE,AD = AF,
∴CA - AD = AE - AF,即CD = EF.
∵DE = 2AD + EF,
∴BD = CD + 2AD.
(3) 解:∠BPE + 2∠CPD = 180°
查看更多完整答案,请扫码查看


