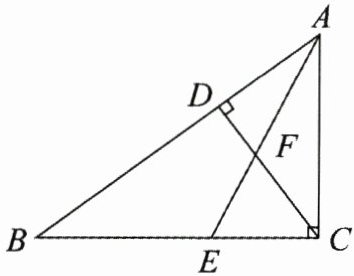
19. 如图,在$ \triangle ABC $中,$ \angle ACB = 90^{\circ} $,$ CD $是$ AB $边上的高,$ AE $是$ \angle BAC $的平分线,$ AE $与$ CD $交于点$ F $. 求证:$ \triangle CEF $是等腰三角形.

答案:
证明:在△ABC中,
∵∠ACB = 90°,
∴∠B + ∠BAC = 90°.
∵CD是边AB上的高,
∴∠ACD + ∠BAC = 90°.
∴∠B = ∠ACD.
∵AE是∠BAC的平分线,
∴∠BAE = ∠EAC.
∴∠B + ∠BAE = ∠ACD + ∠EAC,
即∠CEF = ∠CFE.
∴CE = CF.
∴△CEF是等腰三角形.
∵∠ACB = 90°,
∴∠B + ∠BAC = 90°.
∵CD是边AB上的高,
∴∠ACD + ∠BAC = 90°.
∴∠B = ∠ACD.
∵AE是∠BAC的平分线,
∴∠BAE = ∠EAC.
∴∠B + ∠BAE = ∠ACD + ∠EAC,
即∠CEF = ∠CFE.
∴CE = CF.
∴△CEF是等腰三角形.
20. 综合实践课上,李老师带领同学们探究了这样的问题:
【课本回顾】
在学习等腰三角形时,学习了定理:在一个三角形中,等边对等角. 反之,等角对等边.
【问题探究】
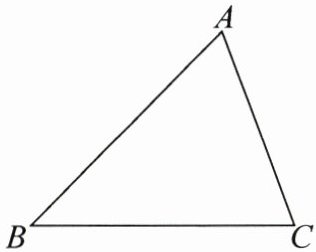
(1)在一个三角形中,如果边不相等,那么其所对的角有什么关系呢?同学们猜测:大边对大角.
如图,在$ \triangle ABC $中,$ AB > AC $. 求证$ \angle C > \angle B $.
经同学们的讨论,小欣同学提出可以利用对称思想解决.
由此,以下三名同学给出了自己的解决方法:
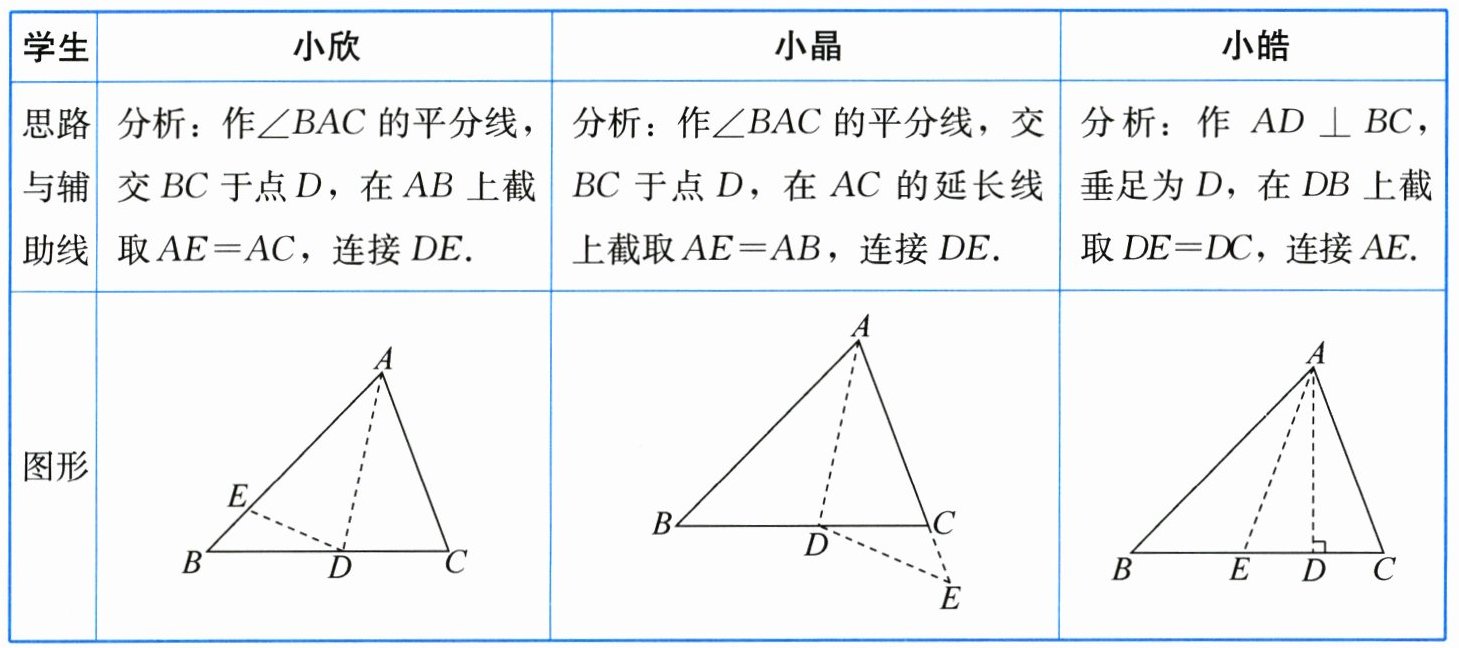
请你用上述同学的思路方法,完整写出其中一个证明.
证明:
【知识应用】
(2)如果一个三角形最大边所对的角是锐角,那么这个三角形是(
A. 锐角三角形
B. 钝角三角形
C. 直角三角形
D. 不能确定
(3)在$ \triangle ABC $中,已知$ AB > BC > CA $,用“$ > $”连接$ \angle A $,$ \angle B $,$ \angle C $应为
【问题拓展】
(4)如果把“在一个三角形中,如果边的长度大,那么边所对的角大”作定理.
①写出这个定理的逆定理:
②证明这个逆定理(要求:画出图形,依照图形写出完整证明过程).
【课本回顾】
在学习等腰三角形时,学习了定理:在一个三角形中,等边对等角. 反之,等角对等边.

【问题探究】
(1)在一个三角形中,如果边不相等,那么其所对的角有什么关系呢?同学们猜测:大边对大角.
如图,在$ \triangle ABC $中,$ AB > AC $. 求证$ \angle C > \angle B $.
经同学们的讨论,小欣同学提出可以利用对称思想解决.
由此,以下三名同学给出了自己的解决方法:

请你用上述同学的思路方法,完整写出其中一个证明.
证明:
【知识应用】
(2)如果一个三角形最大边所对的角是锐角,那么这个三角形是(
A
).A. 锐角三角形
B. 钝角三角形
C. 直角三角形
D. 不能确定
(3)在$ \triangle ABC $中,已知$ AB > BC > CA $,用“$ > $”连接$ \angle A $,$ \angle B $,$ \angle C $应为
∠C > ∠A > ∠B
.【问题拓展】
(4)如果把“在一个三角形中,如果边的长度大,那么边所对的角大”作定理.
①写出这个定理的逆定理:
在一个三角形中,如果角大,那么这个角所对的边长
;②证明这个逆定理(要求:画出图形,依照图形写出完整证明过程).
答案:
(1)(答案不唯一)选择小欣的思路.
证明:作∠BAC的平分线,交BC于点D,在AB上截取AE = AC,连接DE.
∵AD平分∠BAC,
∴∠EAD = ∠CAD.
在△ADE和△ADC中,$\begin{cases}AE = AC \\∠EAD = ∠CAD \\AD = AD\end{cases}$
∴△ADE≌△ADC(SAS).
∴∠AED = ∠C.
∵∠AED是△BDE的外角,
∴∠AED > ∠B.
∴∠C > ∠B.
选择小晶的思路.
证明:作∠BAC的平分线,交BC于点D,在AC的延长线上截取AE = AB,连接DE.
∵AD平分∠BAC,
∴∠BAD = ∠EAD.
又AE = AB,AD = AD,
∴△ABD≌△AED(SAS).
∴∠B = ∠E.
∵∠ACD是△CDE的外角,
∴∠ACD > ∠E.
∴∠ACD > ∠B.
选择小皓的思路.
证明:作AD⊥BC,垂足为D,在DB上截取DE = DC,连接AE.
∵DE = DC,AD⊥BC,
∴AC = AE.
∴∠C = ∠AED.
∵∠AED是△BAE的外角,
∴∠AED > ∠B.
∴∠C > ∠B.
(2) A
(3) ∠C > ∠A > ∠B
(4) ①在一个三角形中,如果角大,那么这个角所对的边长
②已知:在△ABC中,∠C > ∠B.
求证:AB > AC.
证明:如图,在∠ACB的内部,以C为顶点,以CB为一边作∠DCB = ∠B,另一边与AB交于点D.

∵∠DCB = ∠B,
∴BD = CD.
∵AB = AD + BD,
∴AB = AD + CD.
在△ADC中,AD + CD > AC,
∴AB > AC.
(1)(答案不唯一)选择小欣的思路.
证明:作∠BAC的平分线,交BC于点D,在AB上截取AE = AC,连接DE.
∵AD平分∠BAC,
∴∠EAD = ∠CAD.
在△ADE和△ADC中,$\begin{cases}AE = AC \\∠EAD = ∠CAD \\AD = AD\end{cases}$
∴△ADE≌△ADC(SAS).
∴∠AED = ∠C.
∵∠AED是△BDE的外角,
∴∠AED > ∠B.
∴∠C > ∠B.
选择小晶的思路.
证明:作∠BAC的平分线,交BC于点D,在AC的延长线上截取AE = AB,连接DE.
∵AD平分∠BAC,
∴∠BAD = ∠EAD.
又AE = AB,AD = AD,
∴△ABD≌△AED(SAS).
∴∠B = ∠E.
∵∠ACD是△CDE的外角,
∴∠ACD > ∠E.
∴∠ACD > ∠B.
选择小皓的思路.
证明:作AD⊥BC,垂足为D,在DB上截取DE = DC,连接AE.
∵DE = DC,AD⊥BC,
∴AC = AE.
∴∠C = ∠AED.
∵∠AED是△BAE的外角,
∴∠AED > ∠B.
∴∠C > ∠B.
(2) A
(3) ∠C > ∠A > ∠B
(4) ①在一个三角形中,如果角大,那么这个角所对的边长
②已知:在△ABC中,∠C > ∠B.
求证:AB > AC.
证明:如图,在∠ACB的内部,以C为顶点,以CB为一边作∠DCB = ∠B,另一边与AB交于点D.

∵∠DCB = ∠B,
∴BD = CD.
∵AB = AD + BD,
∴AB = AD + CD.
在△ADC中,AD + CD > AC,
∴AB > AC.
查看更多完整答案,请扫码查看


