7. 如图,$ \triangle ABC $是等边三角形,$ AD $是$ BC $边上的中线,$ DE \perp AC $,垂足为$ E $,$ AB = 8 $,则$ CE $的长为(

A.2
B.3
C.4
D.5
A
).
A.2
B.3
C.4
D.5
答案:
A
8. 如图,将$ \triangle ABC $沿$ DE $折叠,$ BD $的对应边$ B'D $恰好经过顶点$ A $,$ \triangle AEB' \cong \triangle DCA $,设$ \angle B = \alpha $,$ \angle C = \beta $,则下列等式成立的是(

A.$ \alpha + \beta = 90^{\circ} $
B.$ 3\alpha + 2\beta = 180^{\circ} $
C.$ 2\alpha = \beta $
D.$ 3\alpha = 2\beta $
B
).
A.$ \alpha + \beta = 90^{\circ} $
B.$ 3\alpha + 2\beta = 180^{\circ} $
C.$ 2\alpha = \beta $
D.$ 3\alpha = 2\beta $
答案:
B
9. 如图,在$ \triangle ABC $中,$ AB = 6 cm $,$ BC = 5 cm $,$ \angle B = 60^{\circ} $,动点$ M $,$ N $分别从点$ B $,$ C $同时出发,其中点$ M $以$ 2 cm/s $的速度沿$ BA $向点$ A $匀速运动,点$ N $以$ 1 cm/s $的速度沿$ CB $向点$ B $匀速运动,当$ M $,$ N $其中一点到达终点时,另一点也随之停止运动,设运动时间为$ t s $,当$ \triangle BMN $为直角三角形时,$ t $的值为(

A.1
B.1或$ \frac{5}{2} $
C.1或2
D.2或$ \frac{5}{2} $
B
).
A.1
B.1或$ \frac{5}{2} $
C.1或2
D.2或$ \frac{5}{2} $
答案:
B
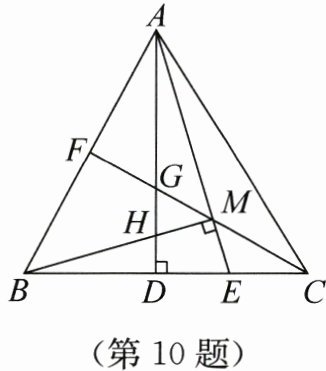
10. 如图,$ AD $,$ CF $分别是$ \triangle ABC $的高和角平分线,$ AD $与$ CF $相交于点$ G $,$ AE $平分$ \angle CAD $交$ BC $于点$ E $,交$ CF $于点$ M $,连接$ BM $交$ AD $于点$ H $,且$ BM \perp AE $. 则下列结论正确的有(
① $ \angle AMC = 135^{\circ} $;② $ \triangle ABC $是等边三角形;③ $ \triangle AMH \cong \triangle BME $;
④ $ BC = BH + 2MH $;⑤ $ S_{\triangle AHM} + S_{\triangle AFM} + S_{\triangle CEM} = \frac{1}{2}S_{\triangle ABC} $.
A.2个
B.3个
C.4个
D.5个
B
).① $ \angle AMC = 135^{\circ} $;② $ \triangle ABC $是等边三角形;③ $ \triangle AMH \cong \triangle BME $;
④ $ BC = BH + 2MH $;⑤ $ S_{\triangle AHM} + S_{\triangle AFM} + S_{\triangle CEM} = \frac{1}{2}S_{\triangle ABC} $.

A.2个
B.3个
C.4个
D.5个
答案:
B
查看更多完整答案,请扫码查看


