18. 如图,在$\triangle ABC$中,$AD$平分$\angle BAC$.
(1)尺规作图:作线段$AD$的垂直平分线$EF$,垂足为点$O$,分别交$AB$,$AC$于点$E$,$F$. 连接$DF$(保留作图痕迹,不要求写作法);
(2)在(1)的条件下,猜想线段$DF$与$AE$的关系,并说明理由.
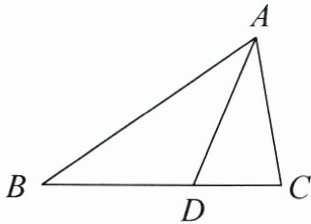
(1)尺规作图:作线段$AD$的垂直平分线$EF$,垂足为点$O$,分别交$AB$,$AC$于点$E$,$F$. 连接$DF$(保留作图痕迹,不要求写作法);
(2)在(1)的条件下,猜想线段$DF$与$AE$的关系,并说明理由.

答案:
解:
(1) 如图,直线EF即为所求.
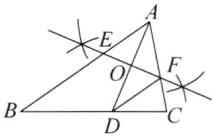
(2) 线段DF与AE平行且相等.
理由如下:
∵ 直线EF为线段AD的垂直平分线,
∴ OA = OD,AF = DF.
∴ ∠DAF = ∠ADF.
∵ AD平分∠BAC,
∴ ∠BAD = ∠FAD.
∴ ∠BAD = ∠ADF.
∴ AE//DF.
在△AOE和△DOF中,
$\begin{cases} ∠BAD = ∠ADF, \\ AO = DO, \\ ∠AOE = ∠DOF, \end{cases}$
∴ △AOE≌△DOF(ASA).
∴ DF = AE.
∴ 线段DF与AE平行且相等.
解:
(1) 如图,直线EF即为所求.

(2) 线段DF与AE平行且相等.
理由如下:
∵ 直线EF为线段AD的垂直平分线,
∴ OA = OD,AF = DF.
∴ ∠DAF = ∠ADF.
∵ AD平分∠BAC,
∴ ∠BAD = ∠FAD.
∴ ∠BAD = ∠ADF.
∴ AE//DF.
在△AOE和△DOF中,
$\begin{cases} ∠BAD = ∠ADF, \\ AO = DO, \\ ∠AOE = ∠DOF, \end{cases}$
∴ △AOE≌△DOF(ASA).
∴ DF = AE.
∴ 线段DF与AE平行且相等.
19. 如图,在等腰三角形$ABC$中,$CA = CB = 4$,$\angle ACB = 120^{\circ}$,点$D$在线段$AB$上运动(不与点$A$,$B$重合),将$\triangle CAD$与$\triangle CBD$分别沿直线$CA$,$CB$翻折得到$\triangle CAP$与$\triangle CBQ$.
(1)求证$CP = CQ$;
(2)求$\angle PCQ$的度数;
(3)当$D$是$AB$的中点时,判断$\triangle DPQ$是何种三角形,并说明理由.
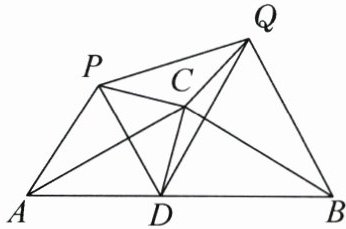
(1)求证$CP = CQ$;
(2)求$\angle PCQ$的度数;
(3)当$D$是$AB$的中点时,判断$\triangle DPQ$是何种三角形,并说明理由.

答案:
(1) 证明:
∵ 将△CAD与△CBD分别沿直线CA,CB翻折得到△CAP与△CBQ,
∴ CP = CD = CQ.
(2) 解:
∵ 将△CAD与△CBD分别沿直线CA,CB翻折得到△CAP与△CBQ,
∴ ∠ACP = ∠ACD,∠BCQ = ∠BCD.
∴ ∠ACP + ∠BCQ = ∠ACD + ∠BCD = ∠ACB = 120°.
∴ ∠PCQ = 360° - (∠ACP + ∠BCQ + ∠ACB) = 360° - (120° + 120°) = 120°.
(3) 解:△DPQ是等边三角形. 理由如下:
∵ 将△CAD与△CBD分别沿直线CA,CB翻折得到△CAP与△CBQ,
∴ AD = AP,∠DAC = ∠PAC.
∵ ∠DAC = $\frac{1}{2}$(180° - ∠ACB) = 30°,
∴ ∠PAD = 60°.
∴ △APD是等边三角形.
∴ PD = AD,∠ADP = 60°.
同理,△BDQ是等边三角形,
∴ DQ = BD,∠BDQ = 60°.
∴ ∠PDQ = 60°.
当D是AB的中点时,AD = BD,
∴ PD = DQ.
∴ △DPQ是等边三角形.
(1) 证明:
∵ 将△CAD与△CBD分别沿直线CA,CB翻折得到△CAP与△CBQ,
∴ CP = CD = CQ.
(2) 解:
∵ 将△CAD与△CBD分别沿直线CA,CB翻折得到△CAP与△CBQ,
∴ ∠ACP = ∠ACD,∠BCQ = ∠BCD.
∴ ∠ACP + ∠BCQ = ∠ACD + ∠BCD = ∠ACB = 120°.
∴ ∠PCQ = 360° - (∠ACP + ∠BCQ + ∠ACB) = 360° - (120° + 120°) = 120°.
(3) 解:△DPQ是等边三角形. 理由如下:
∵ 将△CAD与△CBD分别沿直线CA,CB翻折得到△CAP与△CBQ,
∴ AD = AP,∠DAC = ∠PAC.
∵ ∠DAC = $\frac{1}{2}$(180° - ∠ACB) = 30°,
∴ ∠PAD = 60°.
∴ △APD是等边三角形.
∴ PD = AD,∠ADP = 60°.
同理,△BDQ是等边三角形,
∴ DQ = BD,∠BDQ = 60°.
∴ ∠PDQ = 60°.
当D是AB的中点时,AD = BD,
∴ PD = DQ.
∴ △DPQ是等边三角形.
查看更多完整答案,请扫码查看


