《2025年人教金学典同步解析与测评九年级数学上册人教版重庆专版》

6. 要制作一个母线长为8cm,底面圆周长是$12\pi\mathrm{cm}$的圆锥形小漏斗,若不计损耗,则所需纸板的面积是$48\pi\space cm^2$.

答案： $48\pi\space cm^2$

7. 在如图24.4.2-6所示的圆锥中,$AB$为底面圆的直径,$OA$,$OB$为母线,且$\triangle OAB$是边长为12cm的等边三角形,求这个圆锥的侧面积.

答案： 由题意知，圆锥的底面直径为$AB$，且$\triangle OAB$是边长为$12cm$的等边三角形。
所以圆锥的底面半径$r = \frac{AB}{2} = \frac{12}{2} = 6cm$，
圆锥的母线长$l = OA = 12cm$。
根据圆锥侧面积公式$S = \pi rl$，代入$r = 6cm$，$l = 12cm$，得：
$S = \pi × 6 × 12 = 72\pi cm^2$。
故这个圆锥的侧面积为$72\pi cm^2$。

8. 如图24.4.2-7,现有$30\%$圆周的一个扇形彩纸片,该扇形的半径为40cm.小红为了在元旦联欢晚会上表演节目,她打算剪去部分扇形纸片后,利用剩下的纸片制作一个底面半径为10cm的圆锥形纸帽(接缝处不重叠),那么剪去的扇形纸片的圆心角为(B)

A.$9^{\circ}$
B.$18^{\circ}$
C.$63^{\circ}$
D.$72^{\circ}$

答案： B

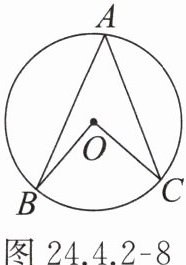
9. 如图24.4.2-8,已知$\odot O$的半径为4,$\angle A = 45^{\circ}$,若一个圆锥的侧面展开图与扇形$OBC$能完全重合,求该圆锥的底面圆的半径.

答案： 1